GIF Animations
OneMax problem:
\(\text{Maximize } f(\boldsymbol{x}) = \sum_{i=1}^n x_i\) \(x_i \in \{0,1\}\) \(f(\boldsymbol{x}^*) = f(1,1,\dots,1) = n\)
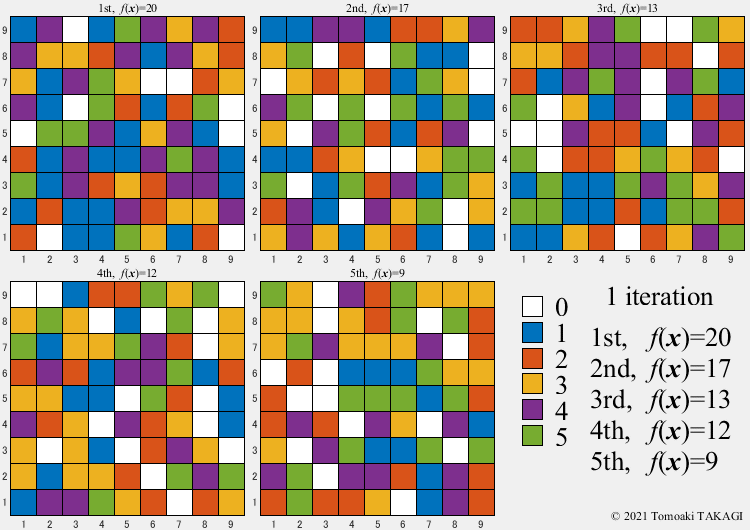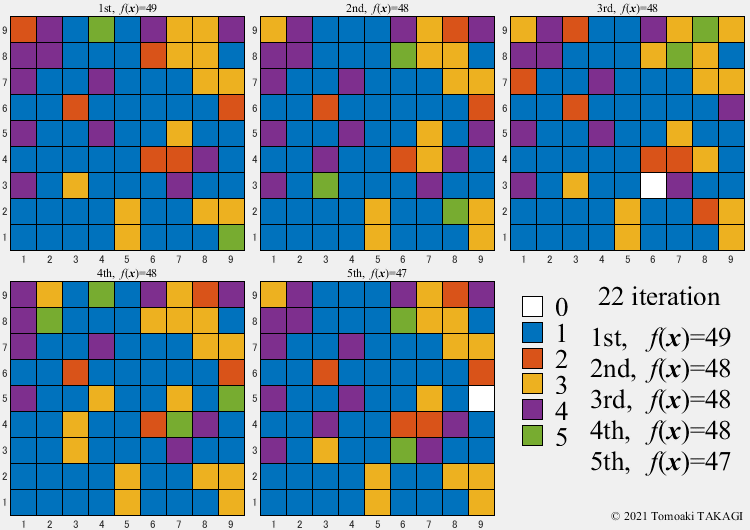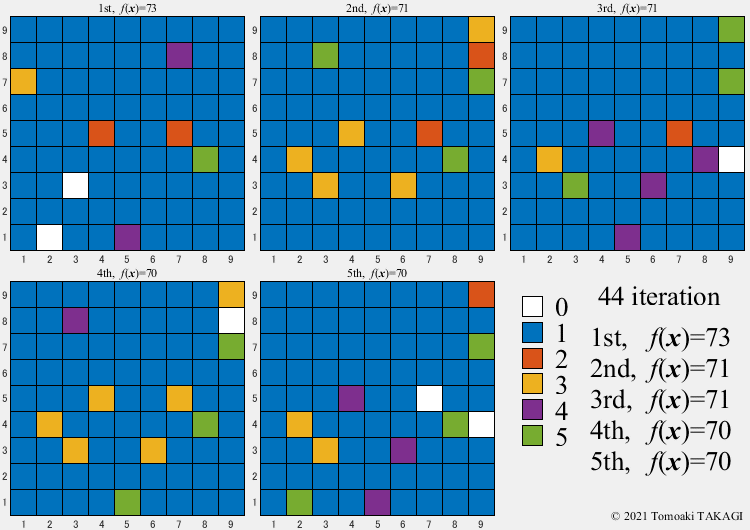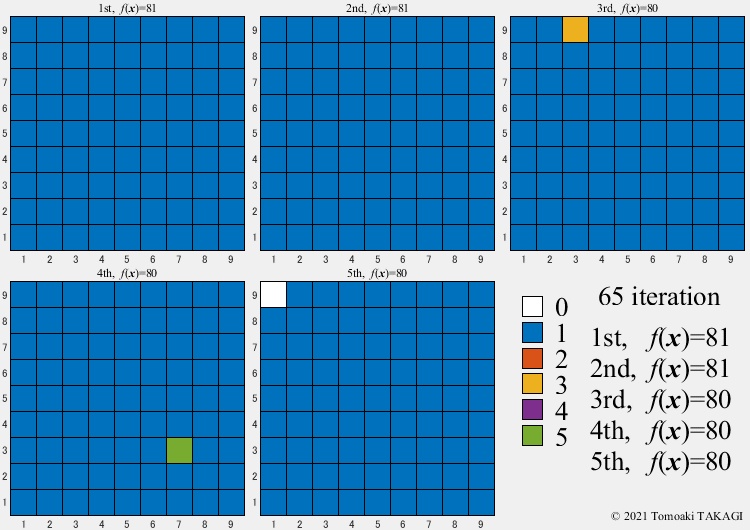
Extended OneMax problem:
\(\text{Maximize } f(\boldsymbol{x}) = \sum_{i=1}^n F(x_i)\) \(F(x_i) = \cases{1 & \text{if } x_i=1\cr 0 & \text{otherwise}}\) \(x_i \in \{0,1,\dots,5\}\) \(f(\boldsymbol{x^*}) = f(1,1,\dots,1) = n\)
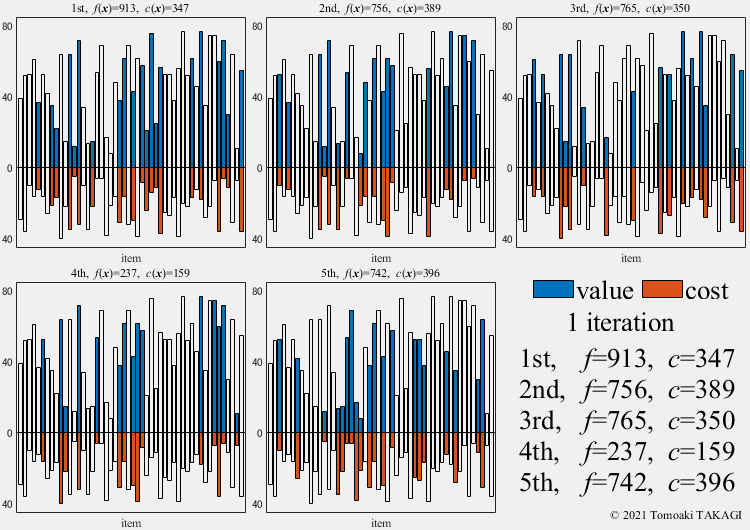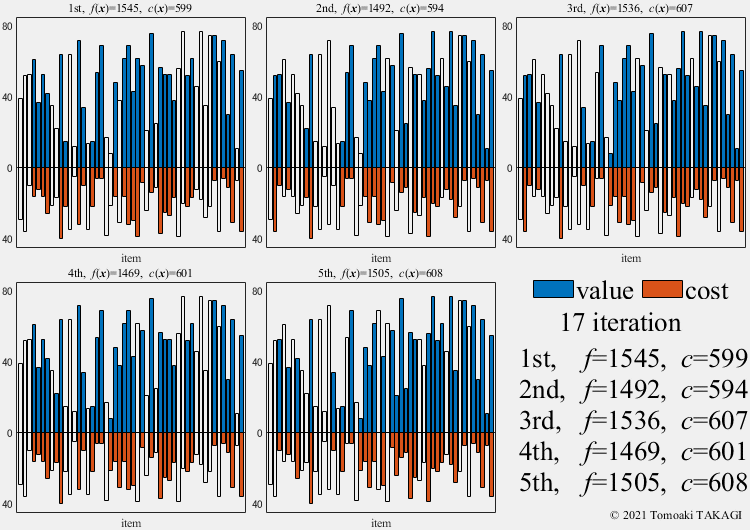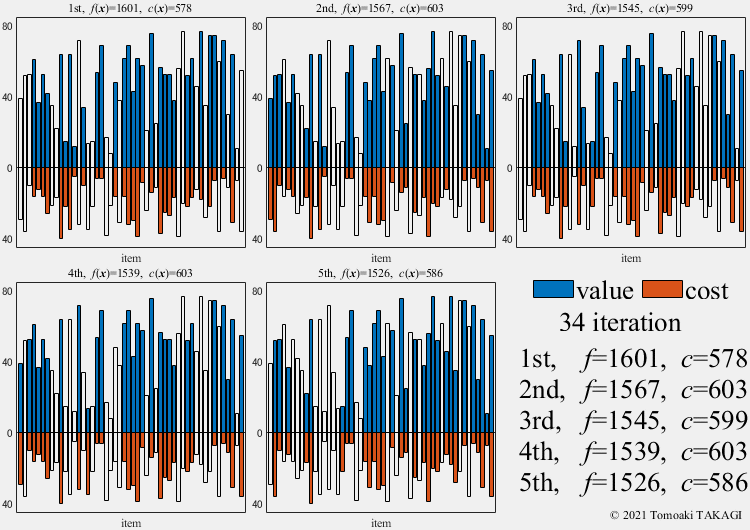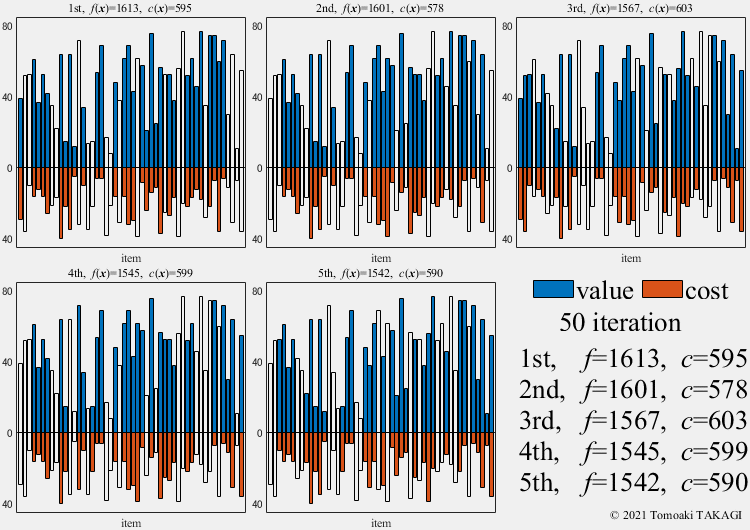
0/1 Knapsack problem:
Given a set of \(n\) items, each with a value \(v_i\) and a cost \(w_i\), along with a maximum capacity \(W(=600)\)
\(\text{Maximize } f(\boldsymbol{x}) = \sum_{i=1}^n v_ix_i\) \(\text{Subject to } c(\boldsymbol{x}) = \sum_{i=1}^n w_ix_i \leq W\) \(x_i \in \{0,1\}\)
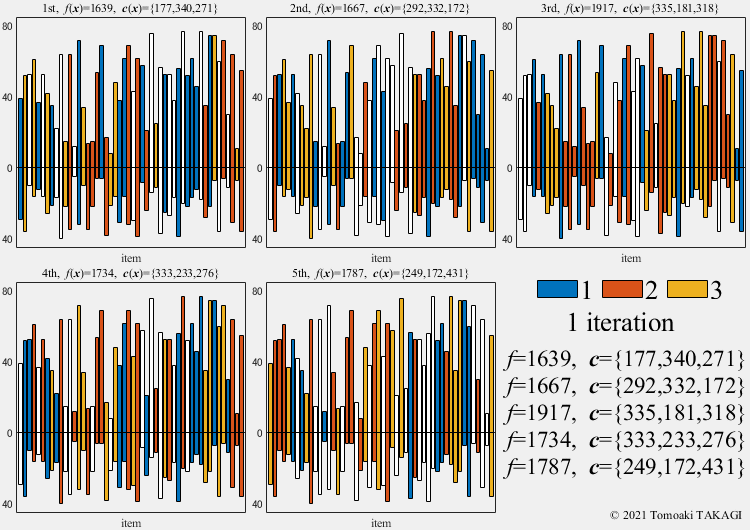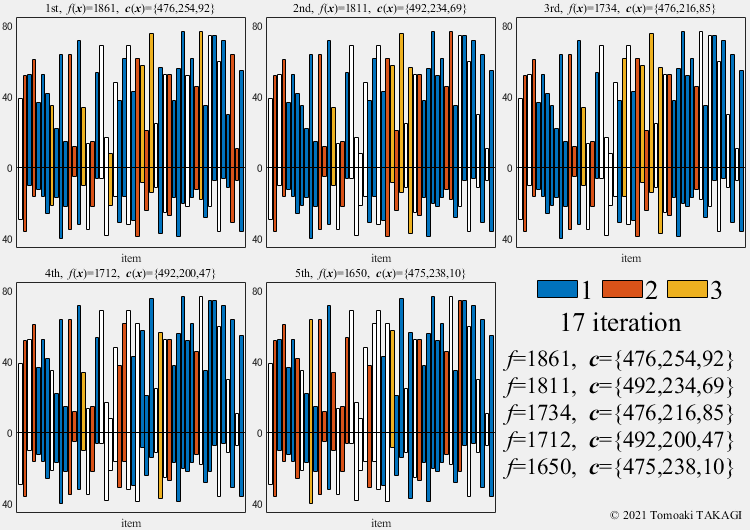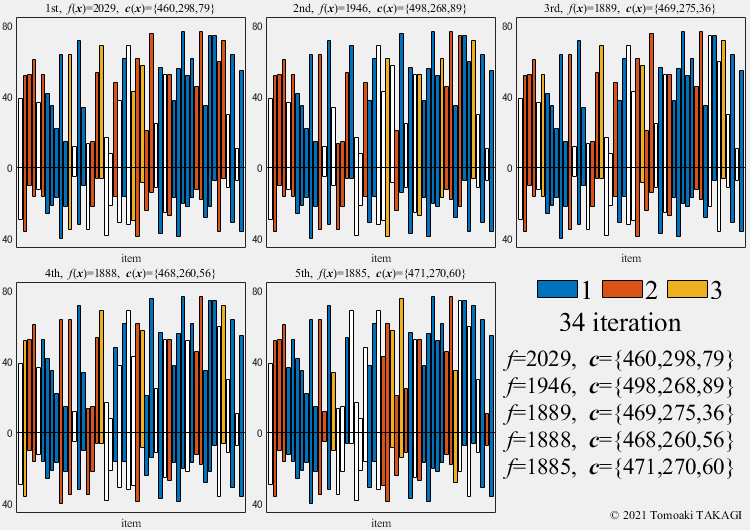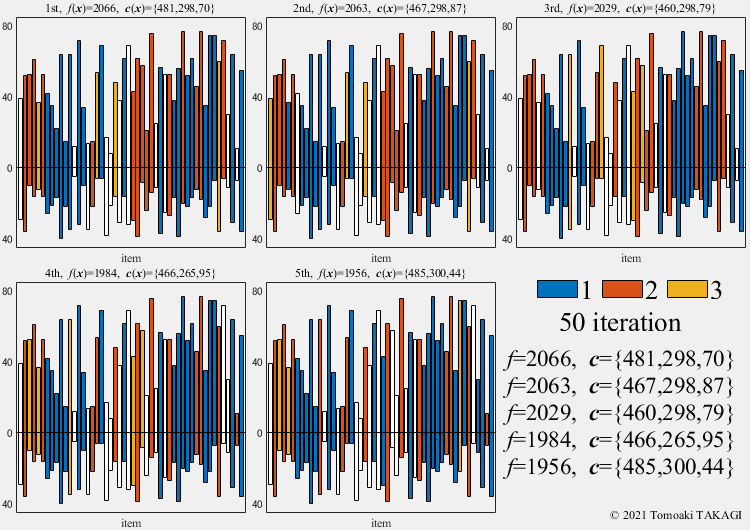
Multiple Knapsack problem:
Given a set of \(n\) items, each with a value \(v_i\) and a cost \(w_i\), along with maximum capacitys \(\boldsymbol{W}(=\{500,300,100\})\)
\(\text{Maximize } f(\boldsymbol{x}) = \sum_{j=1}^3\sum_{i=1}^n v_iF(x_i,j)\) \(F(x_i,j) = \cases{1 & \text{if } x_i=j\cr 0 & \text{otherwise}}\) \(\text{Subject to } c_j(\boldsymbol{x}) = \sum_{i=1}^n w_iF(x_i,j) \leq W_j\) \(x_i \in \{0,1,2,3\}\)
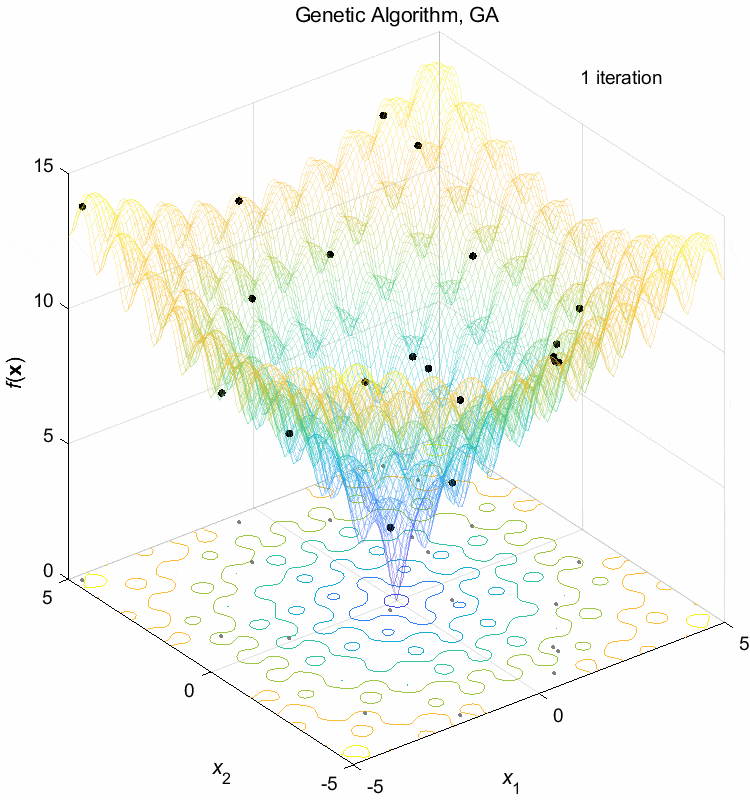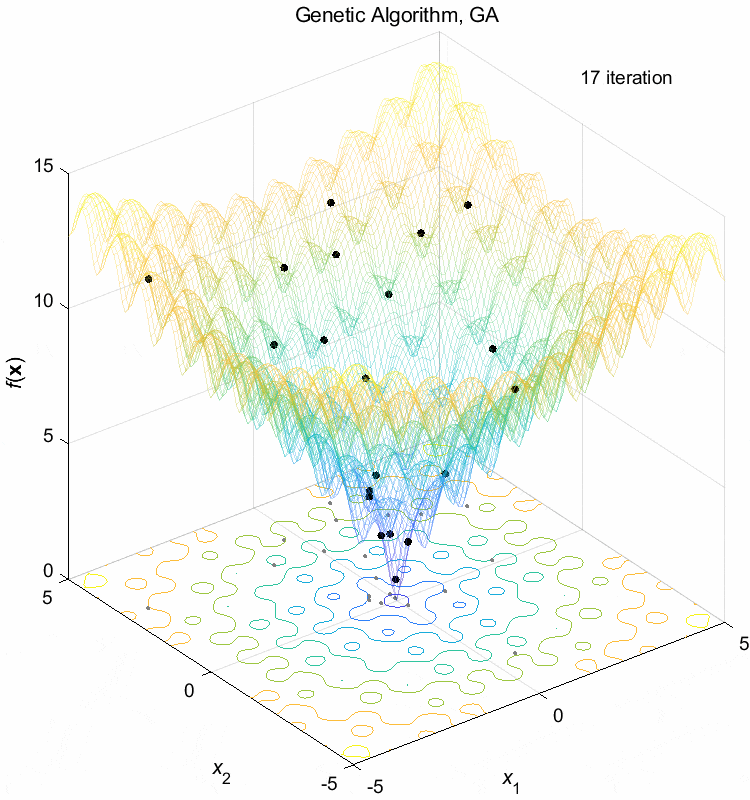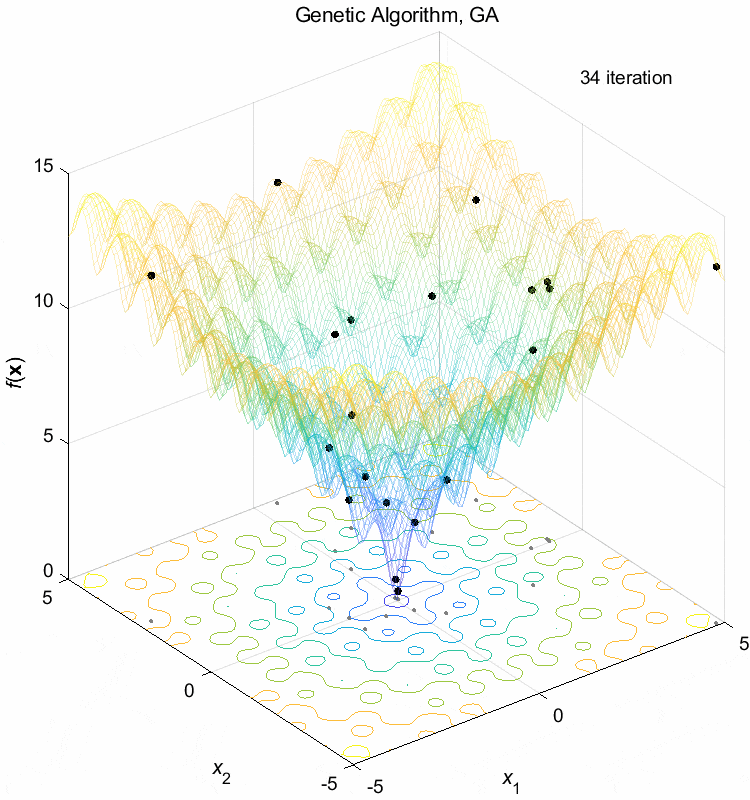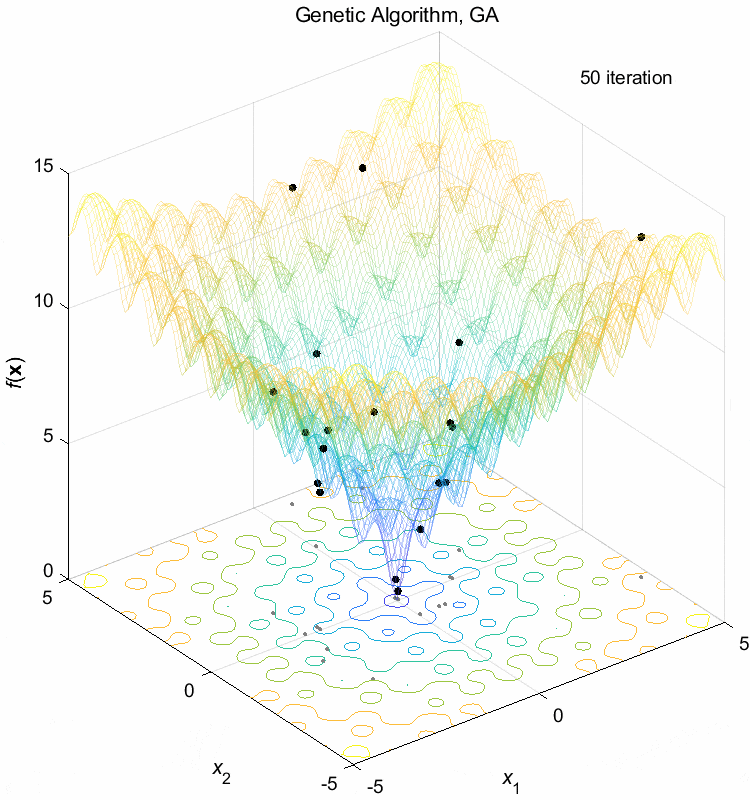
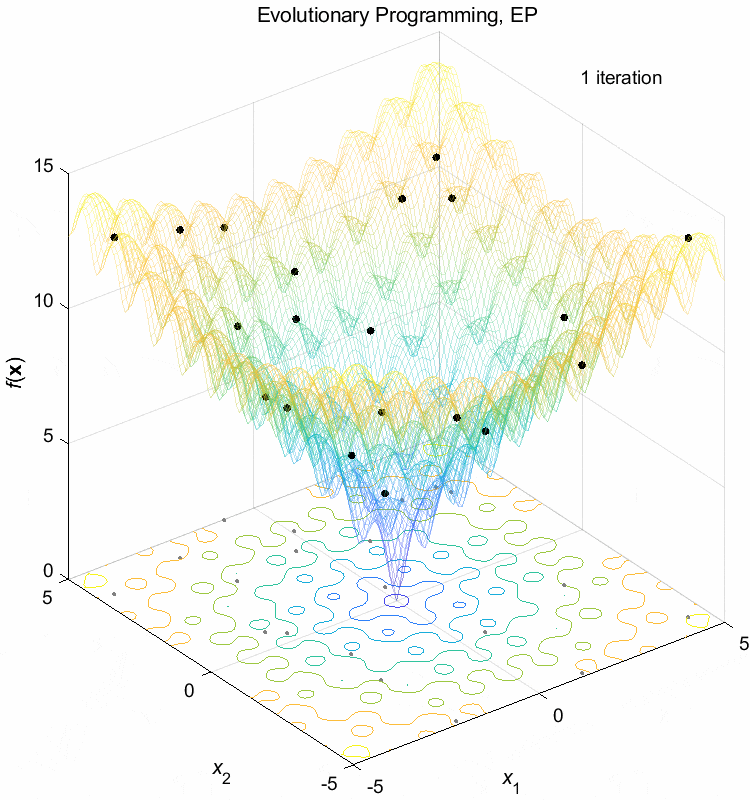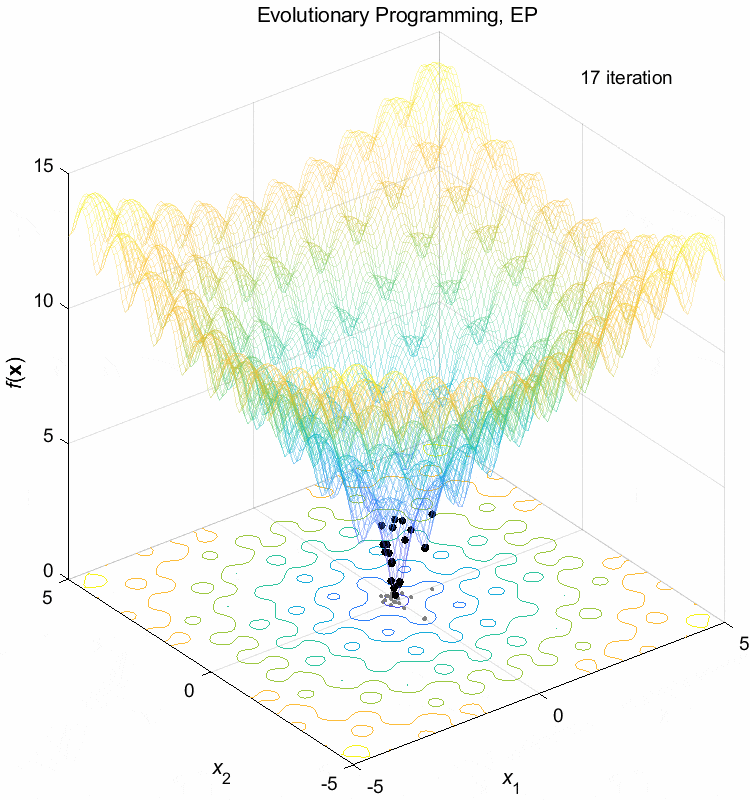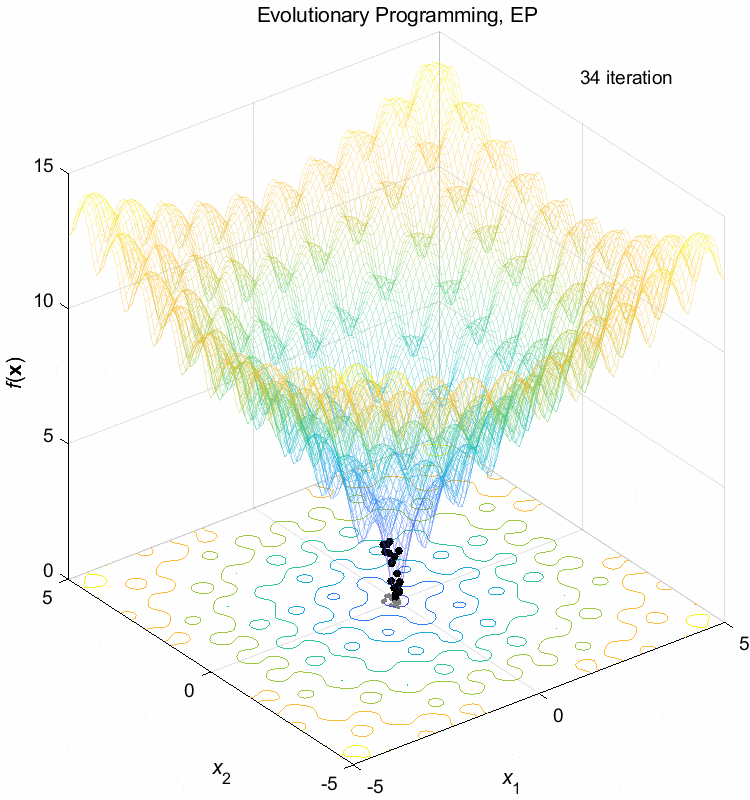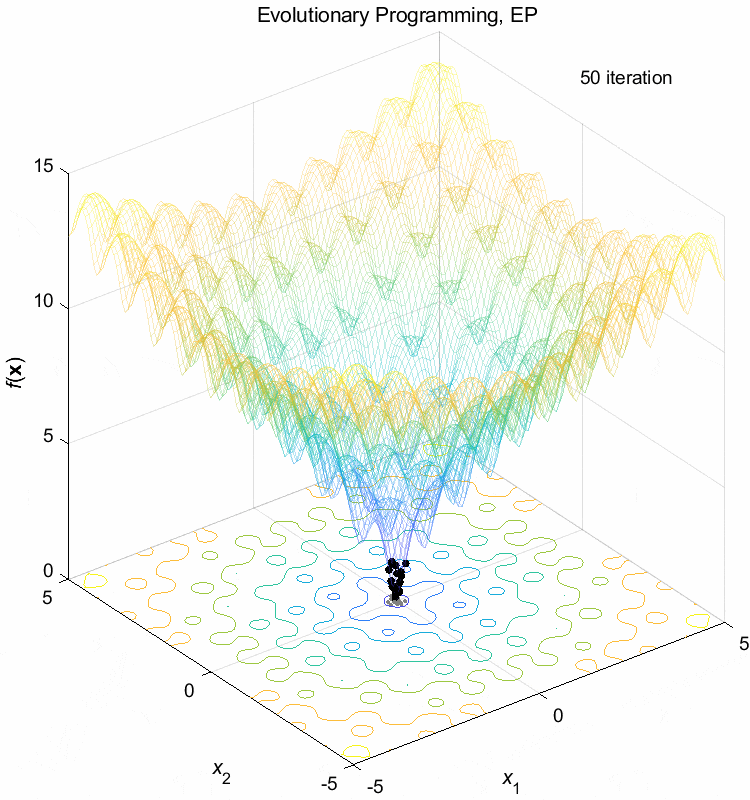
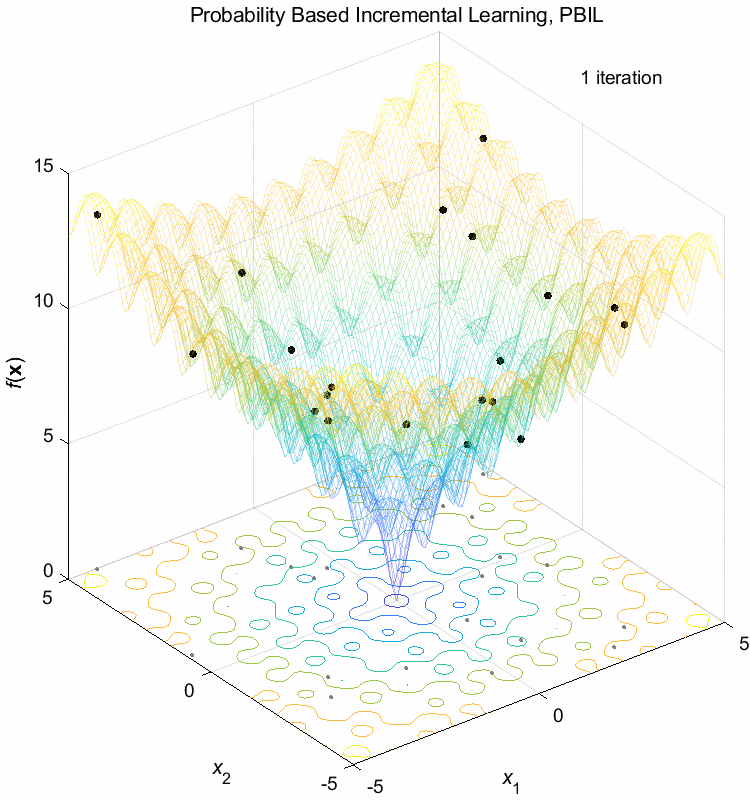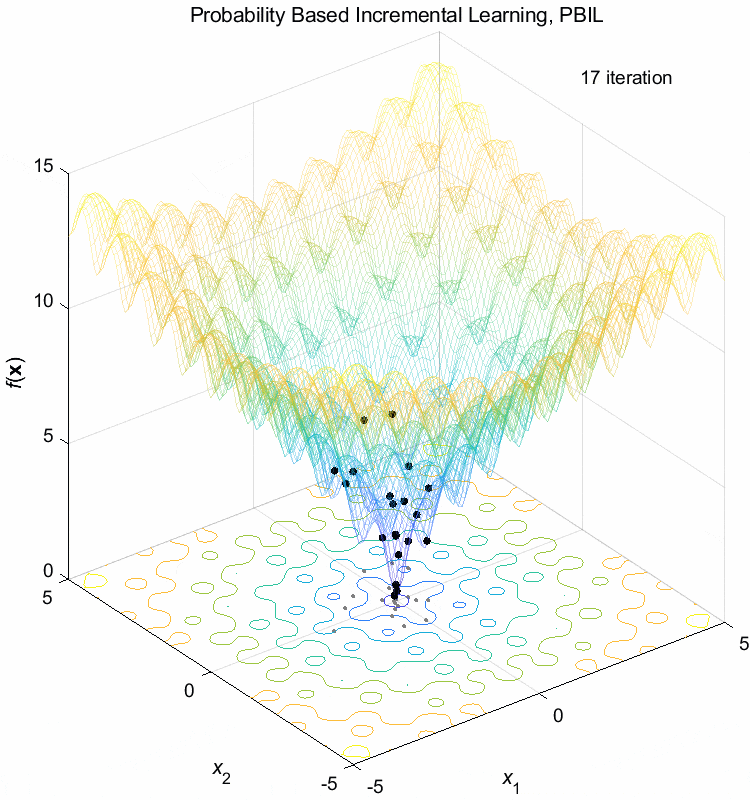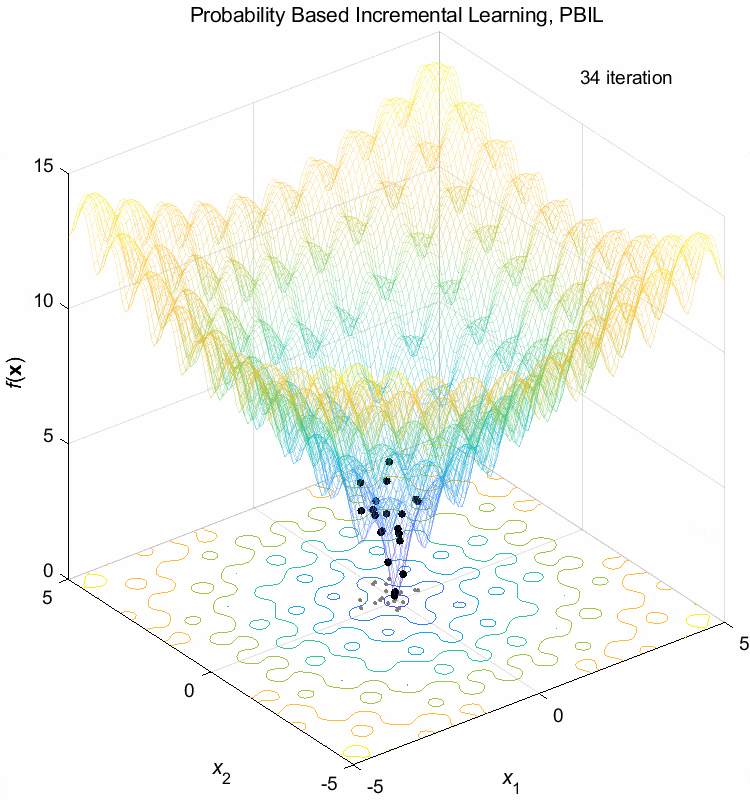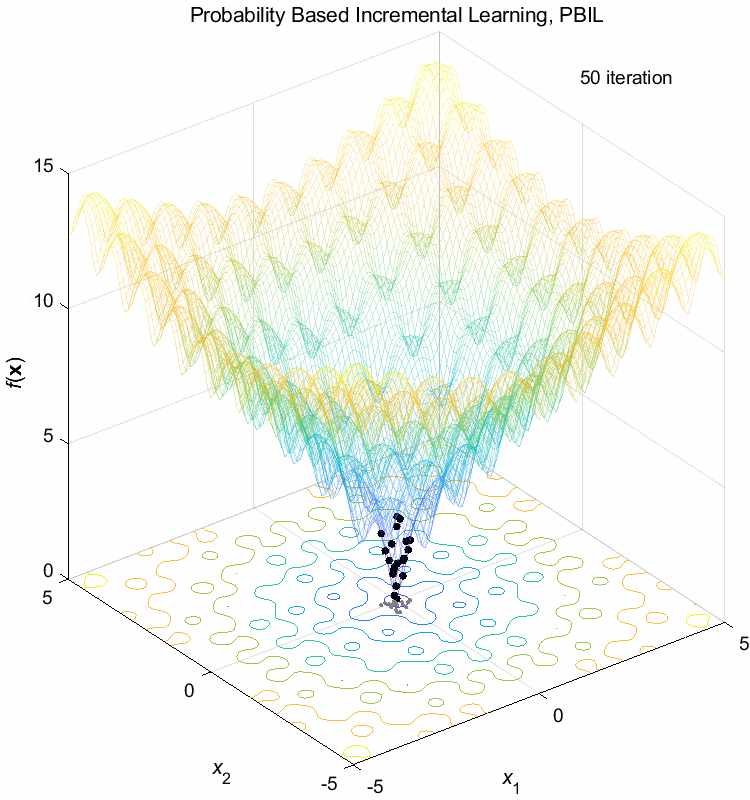
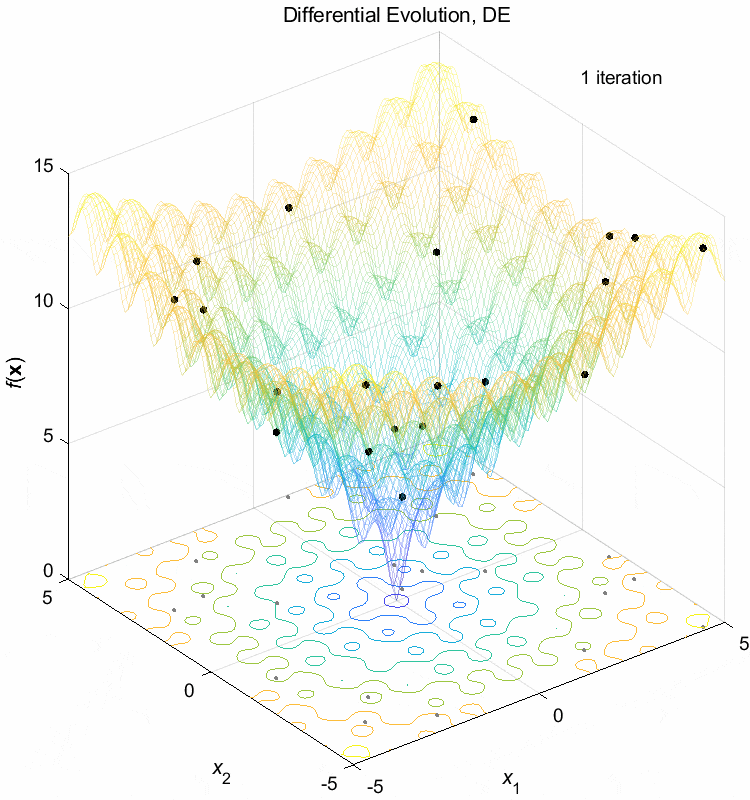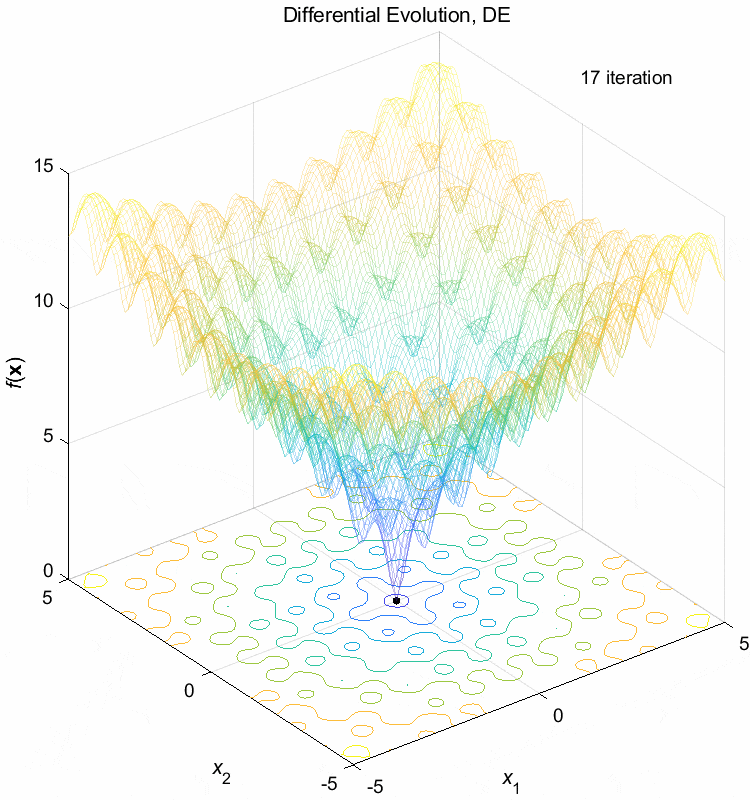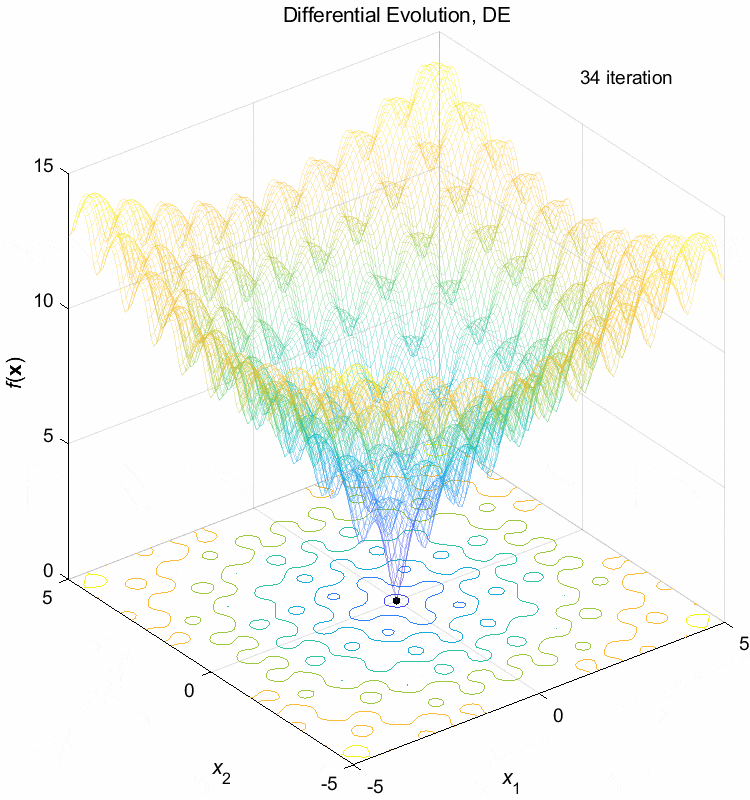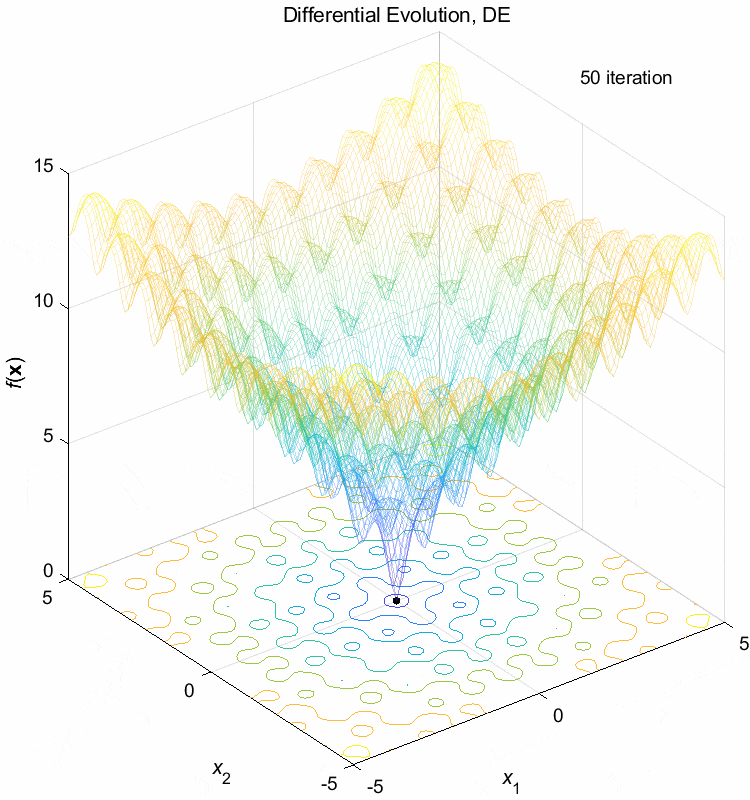
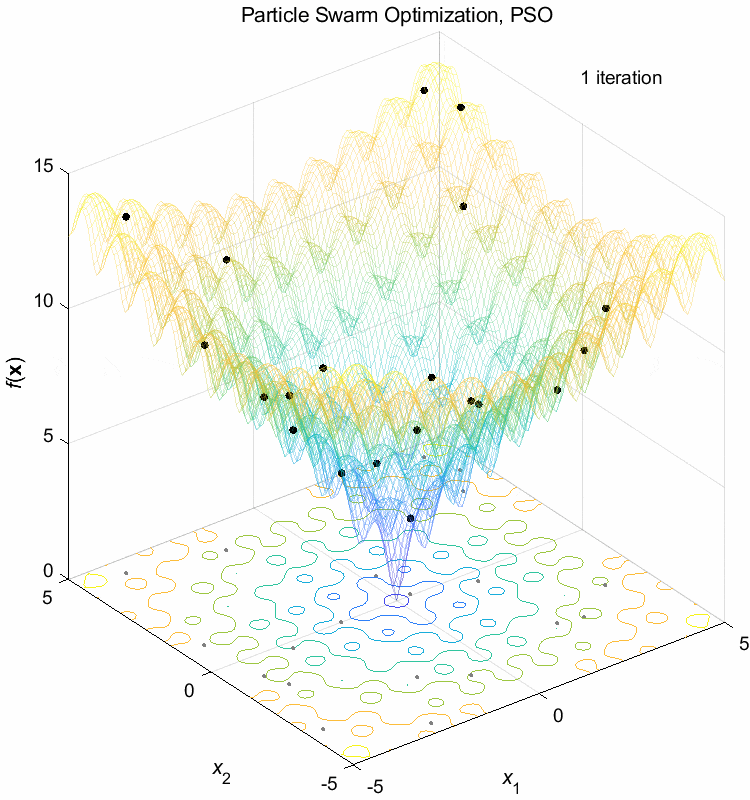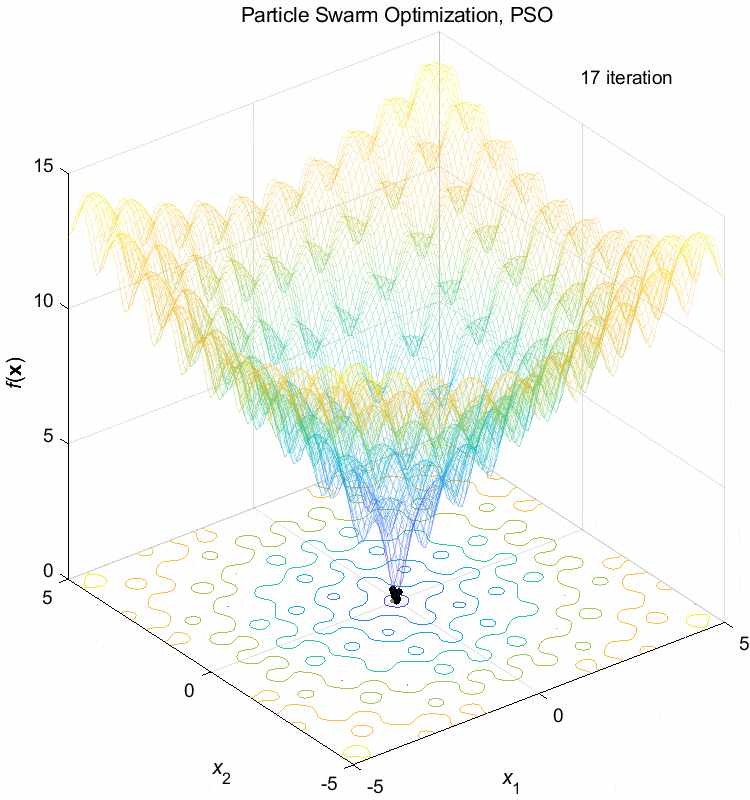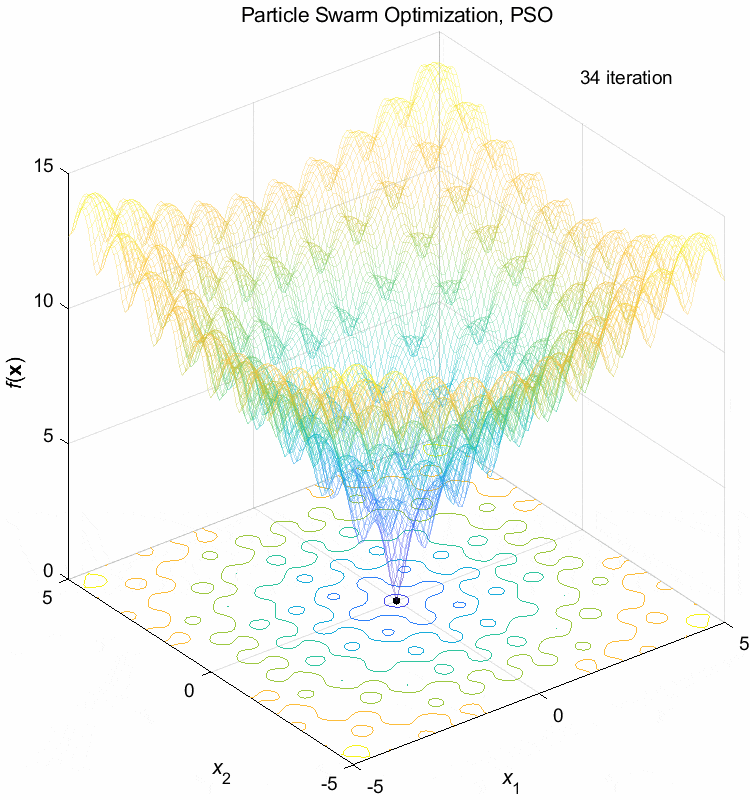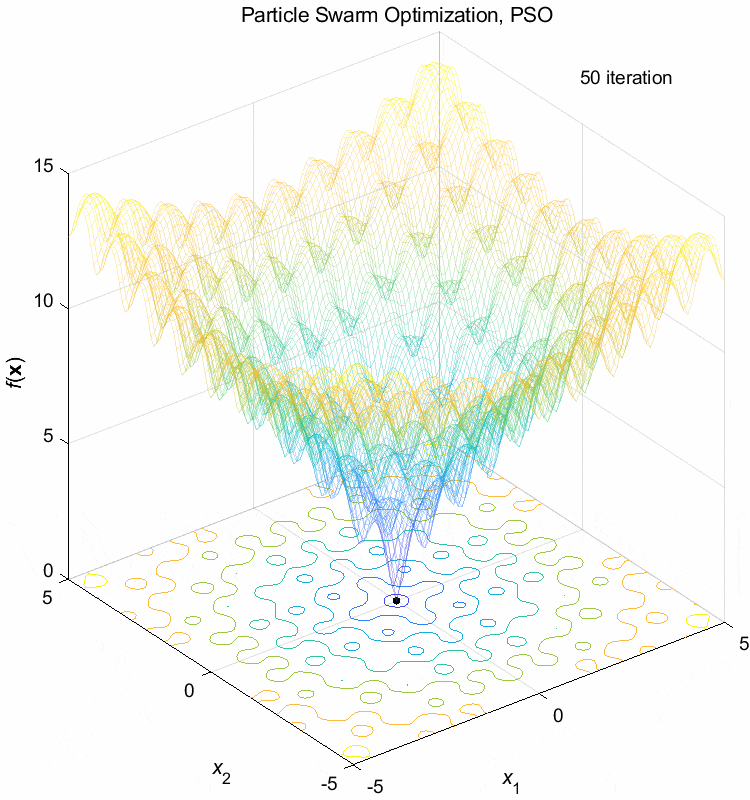
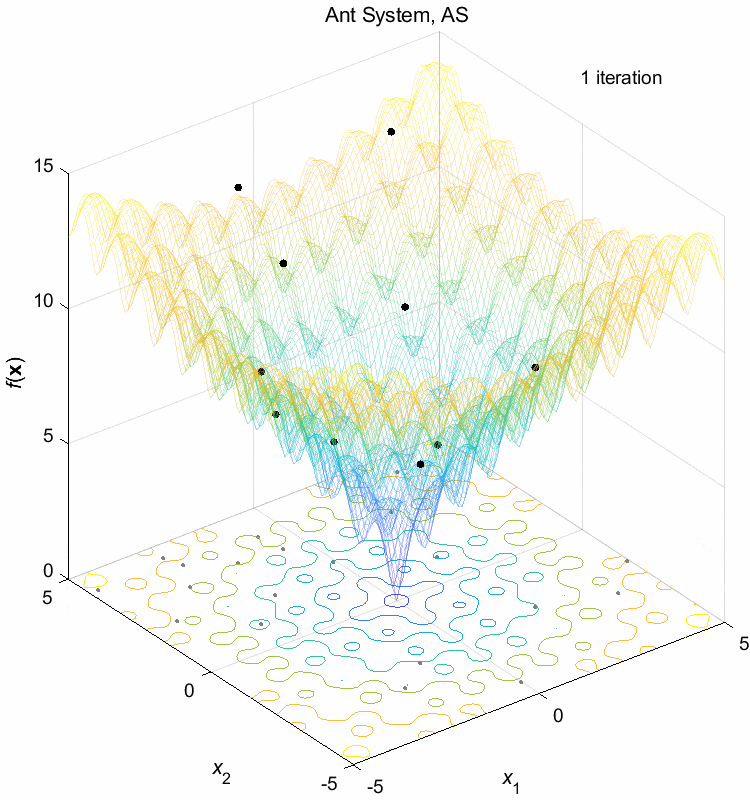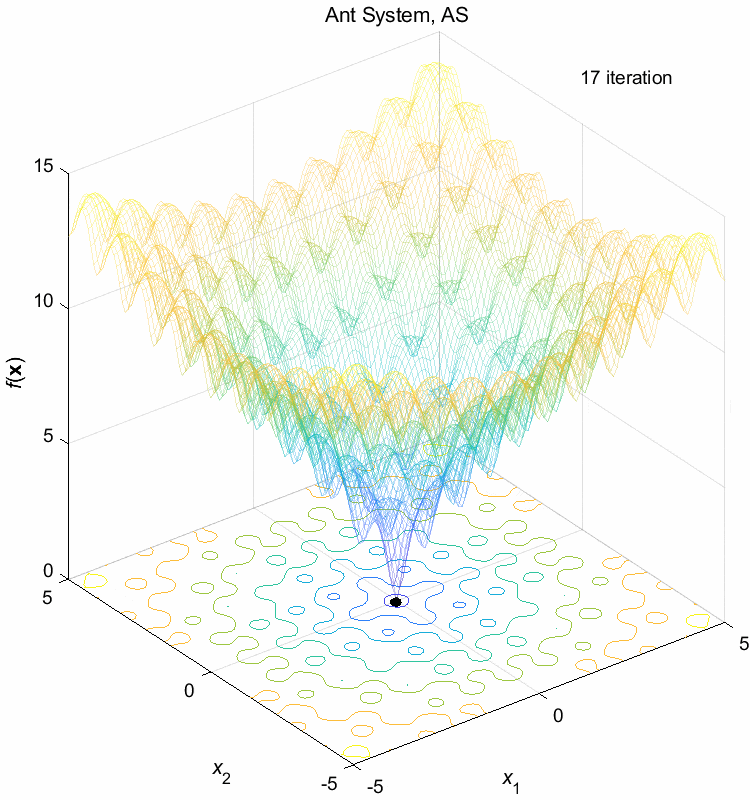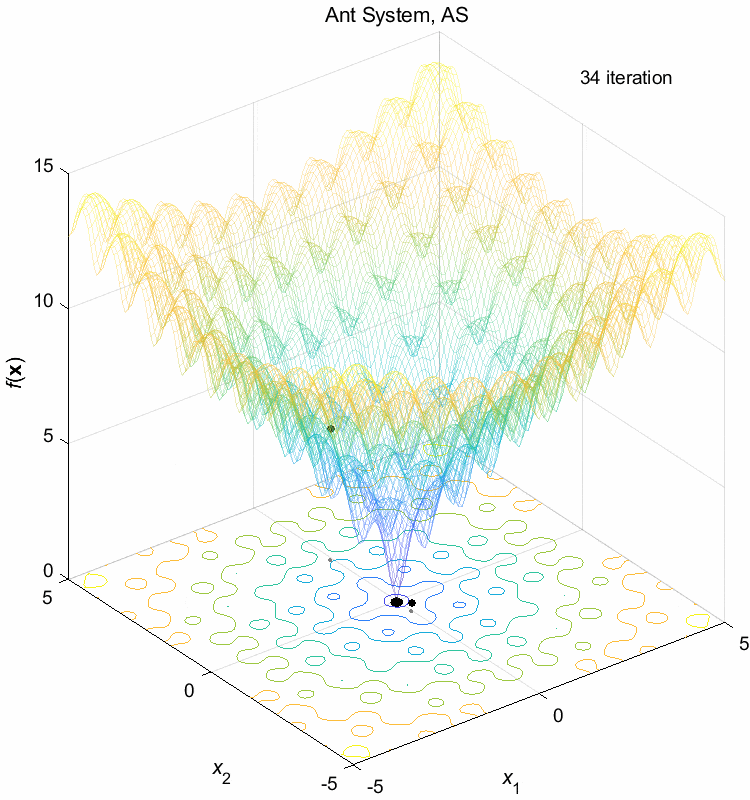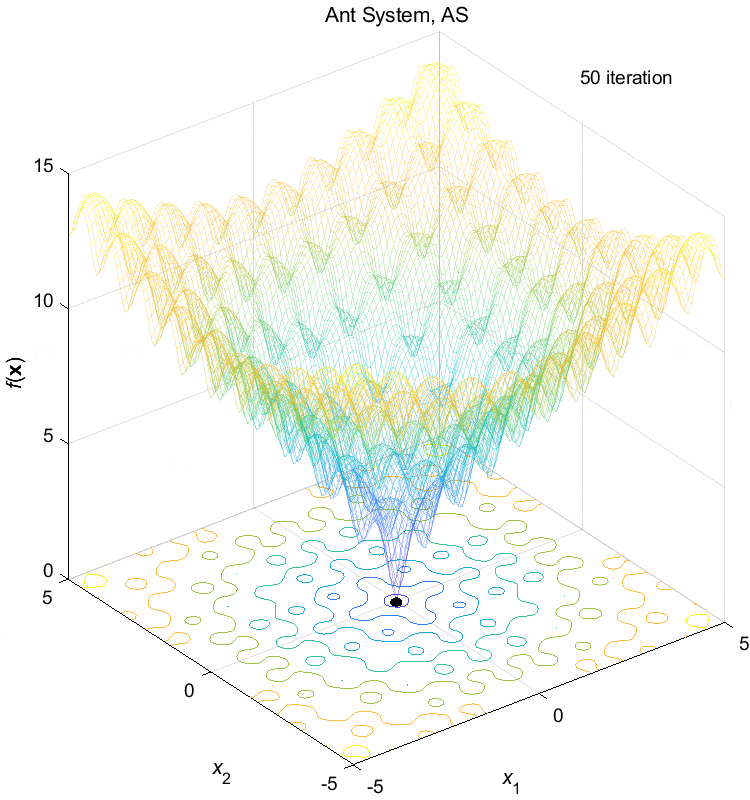
Ackley function:
\(\text{Minimize } f(\boldsymbol{x}) = -20 \exp(-0.2 \sqrt{\frac{1}{n} \sum_{i=1}^n x_i^2}) - \exp(\frac{1}{n} \sum_{i=1}^n \cos(2\pi x_i)) + 20 + \exp(1)\)
\(-5 \leq x_i \leq 5\) \(f(\boldsymbol{x}^*) = f(0,0,\dots,0)=0\)
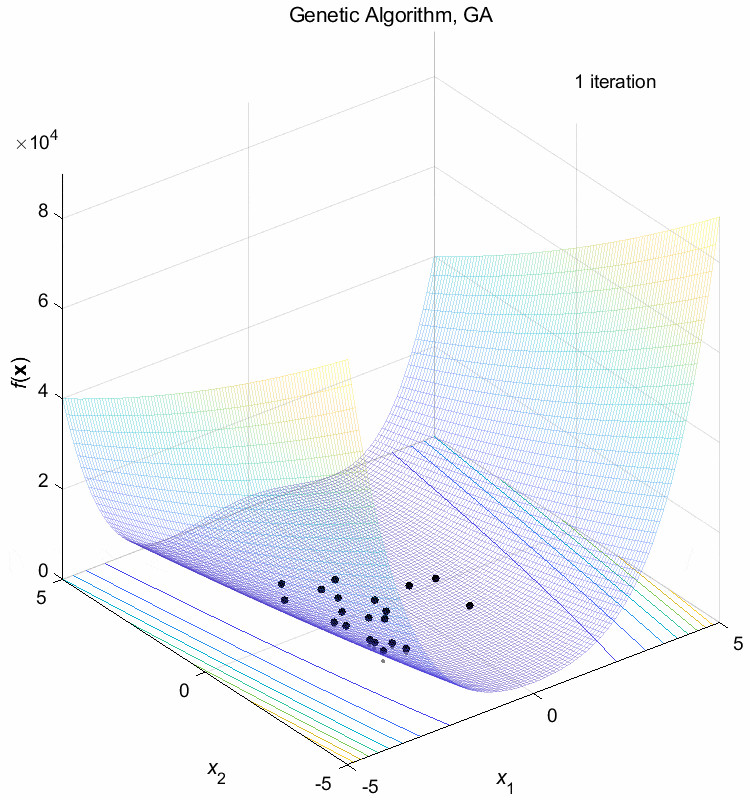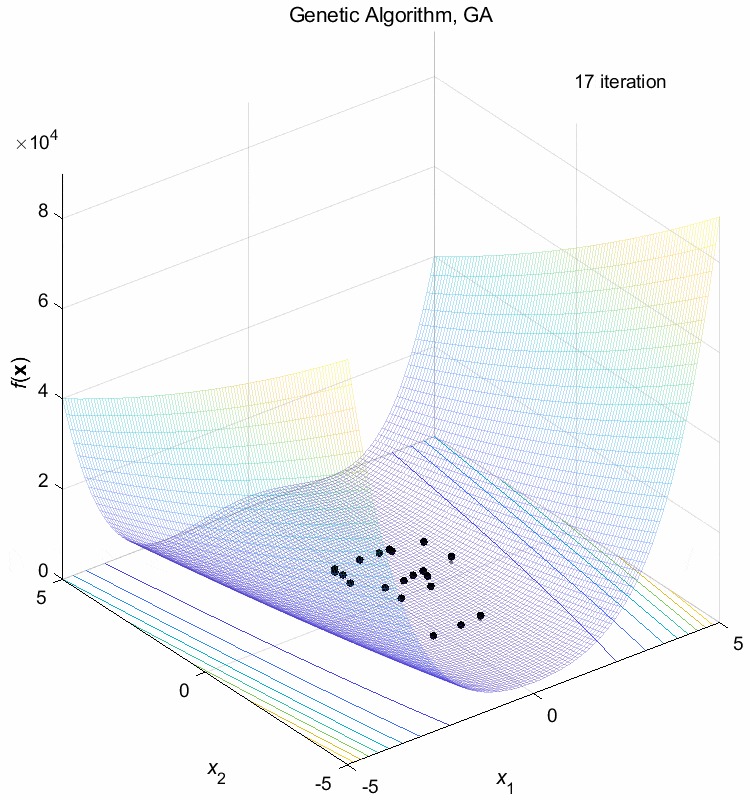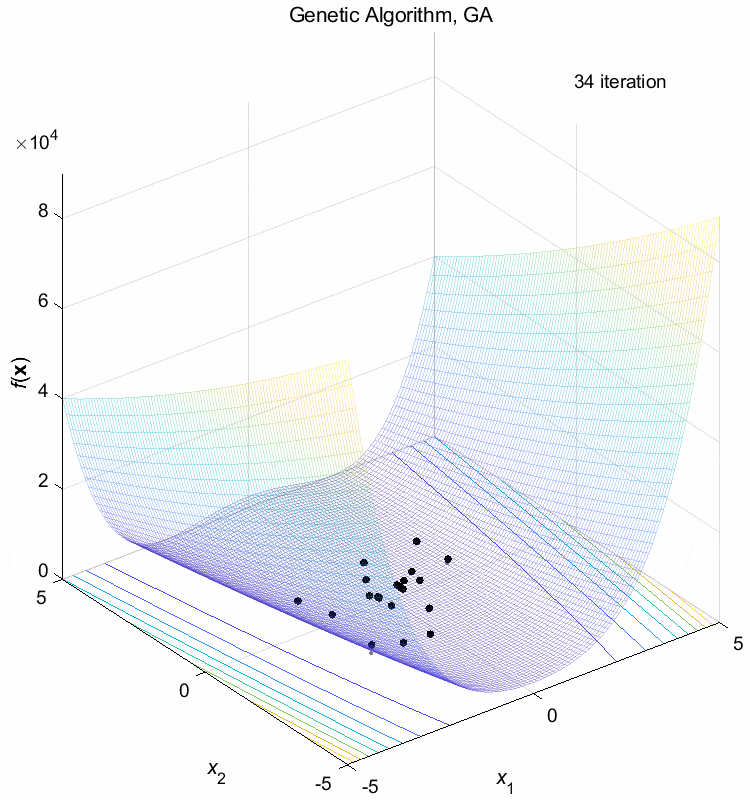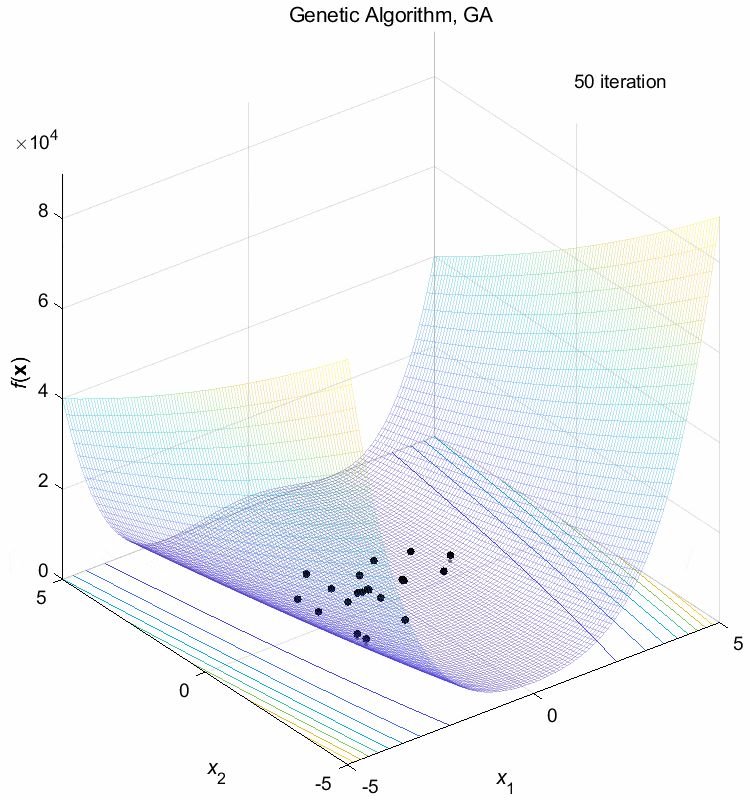
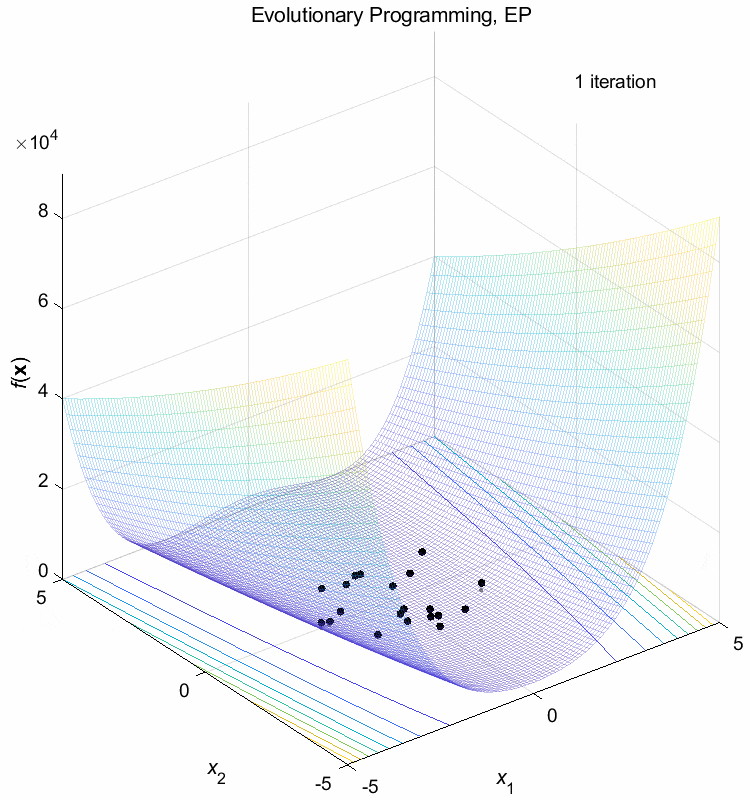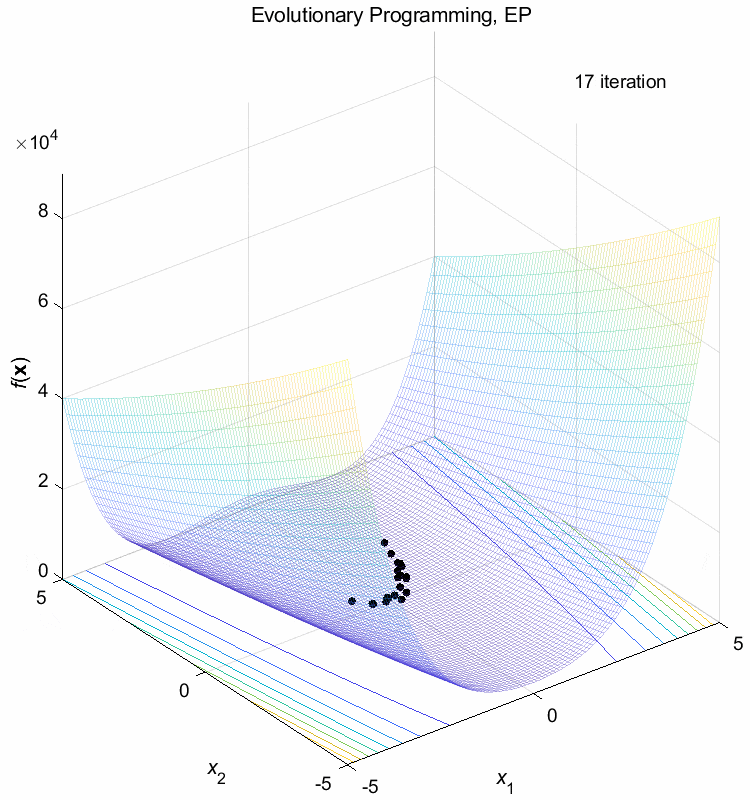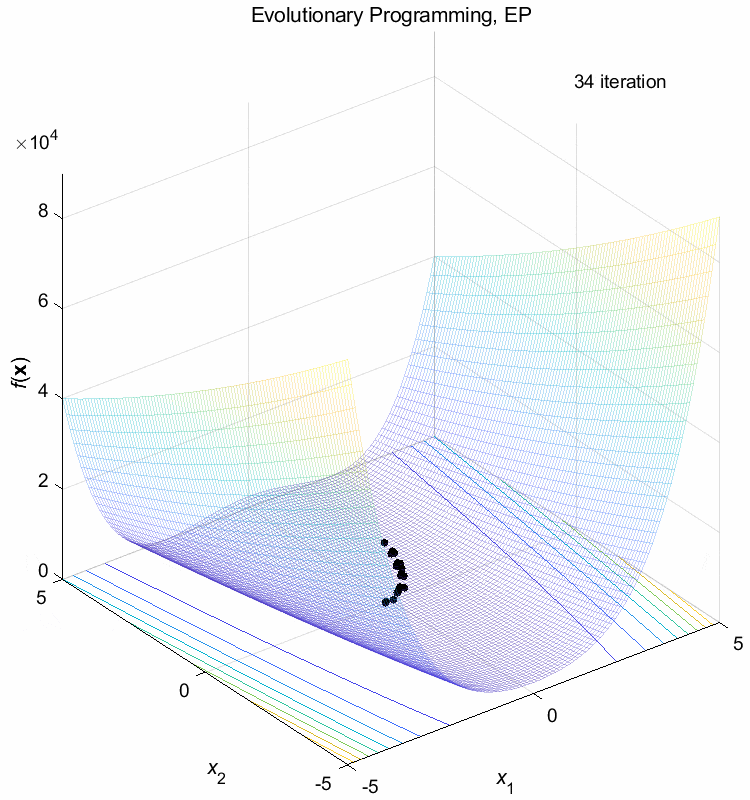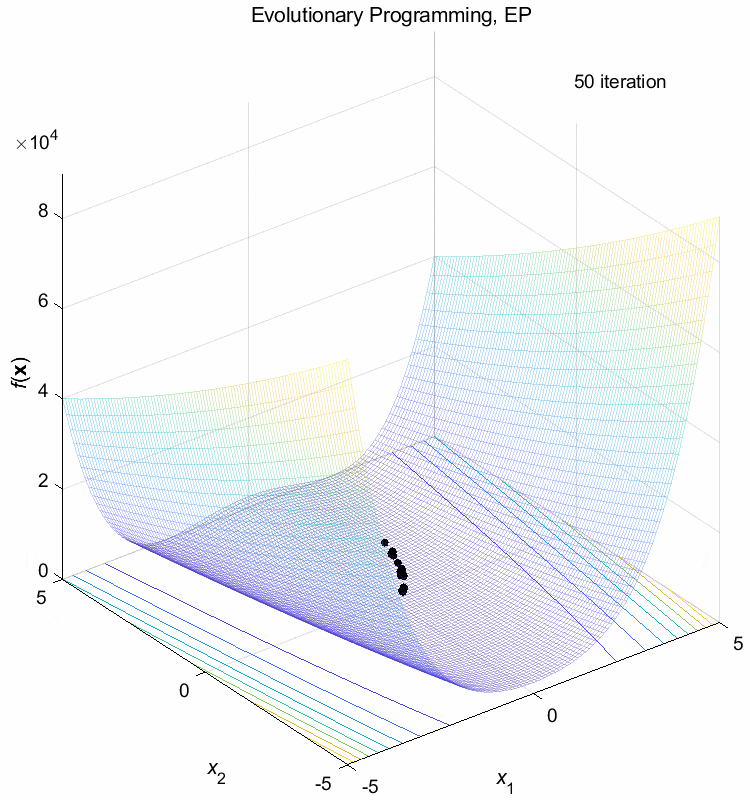
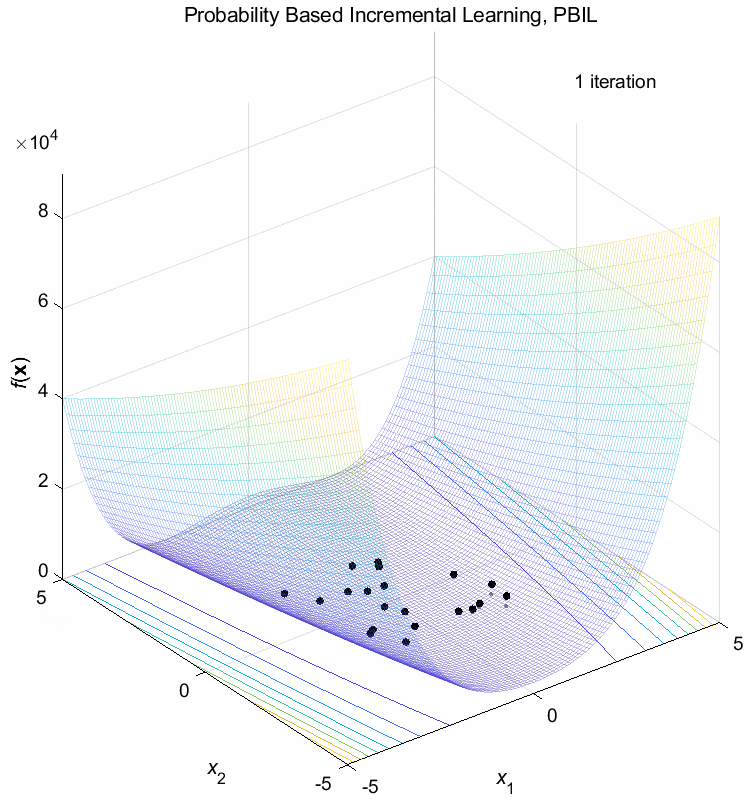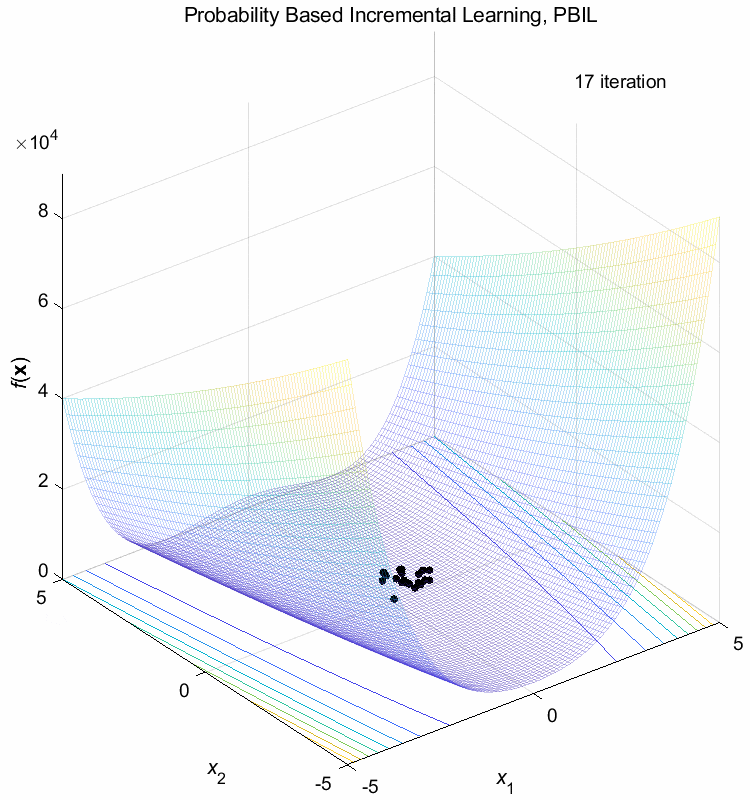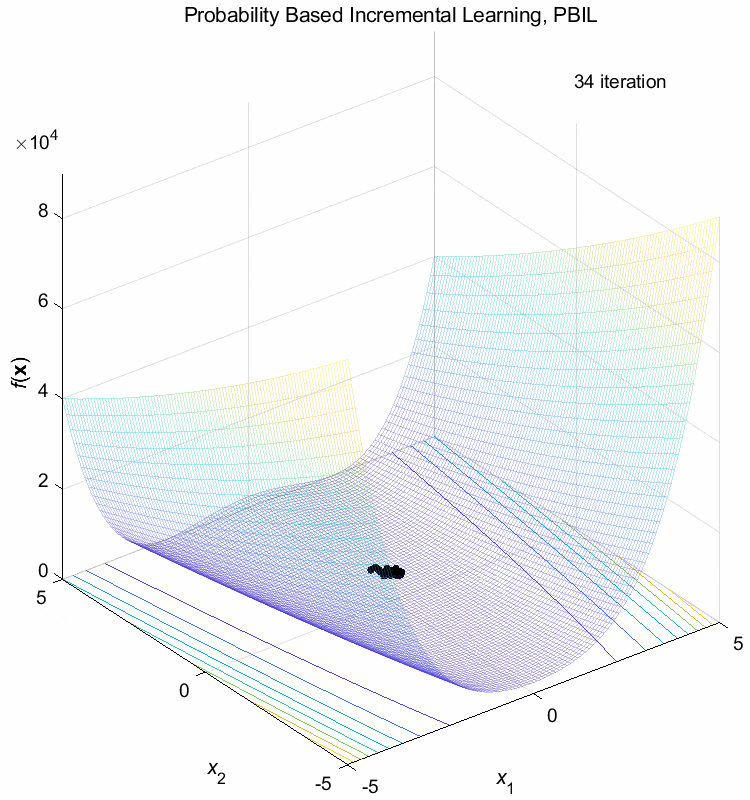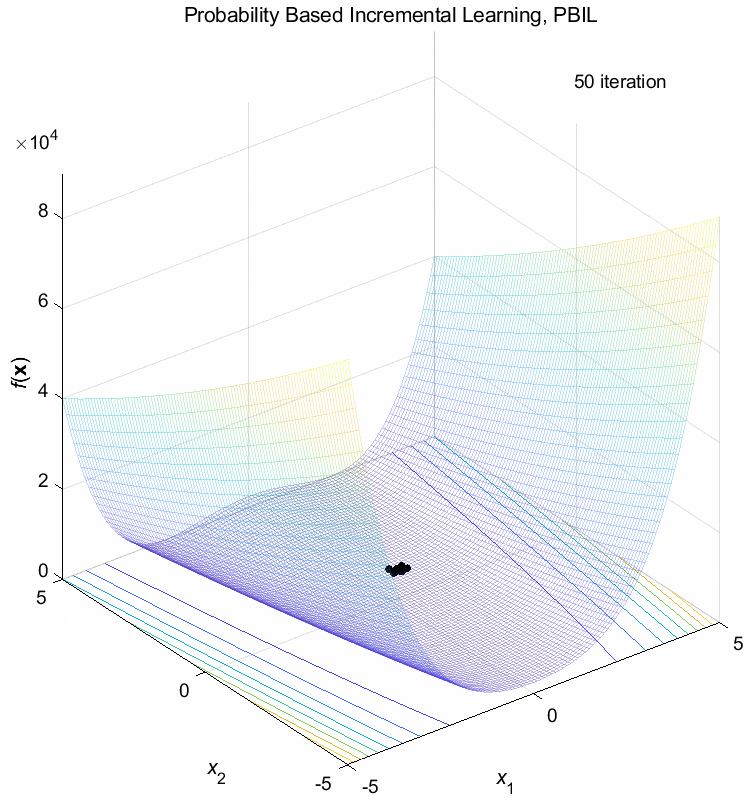
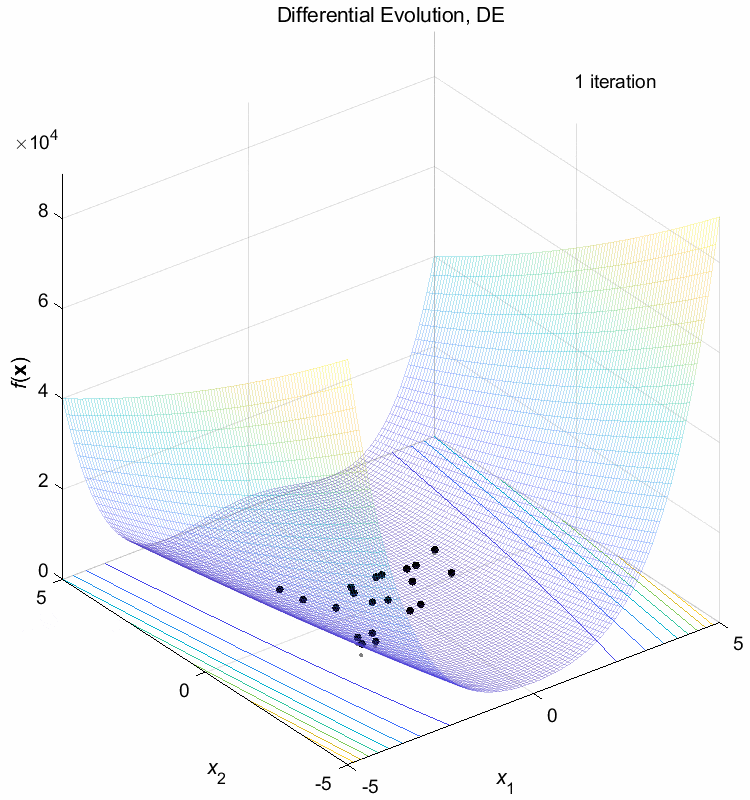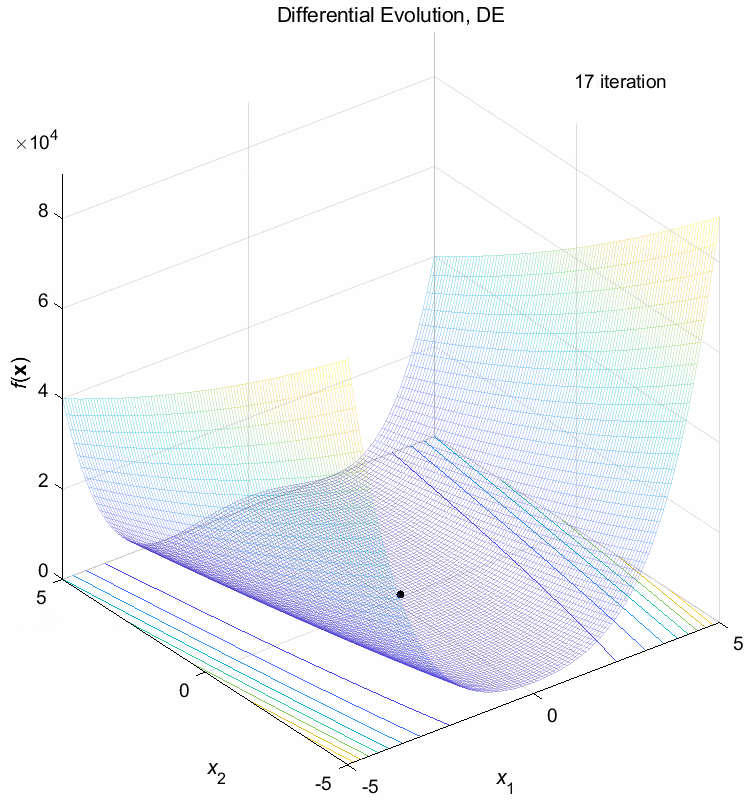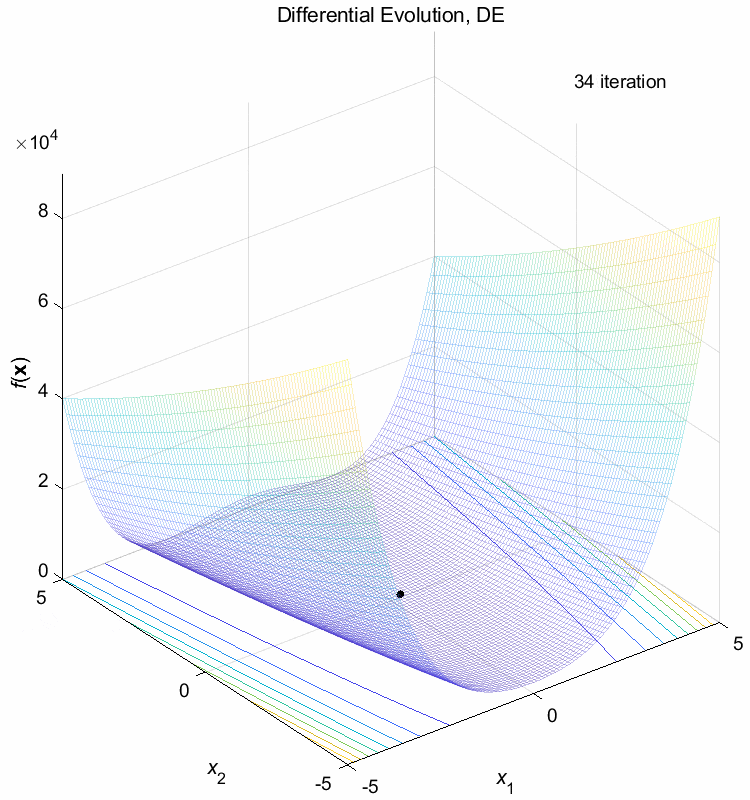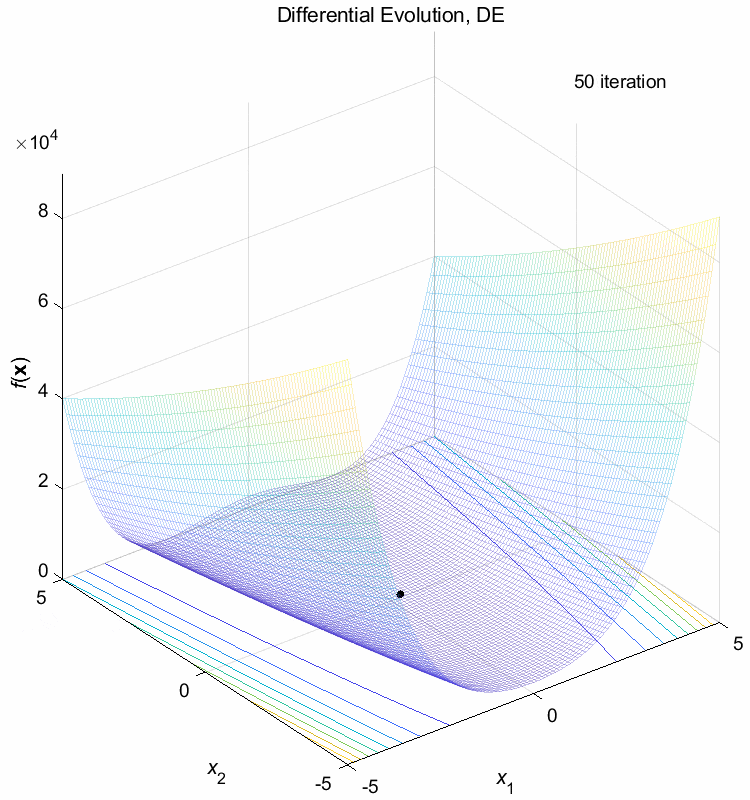
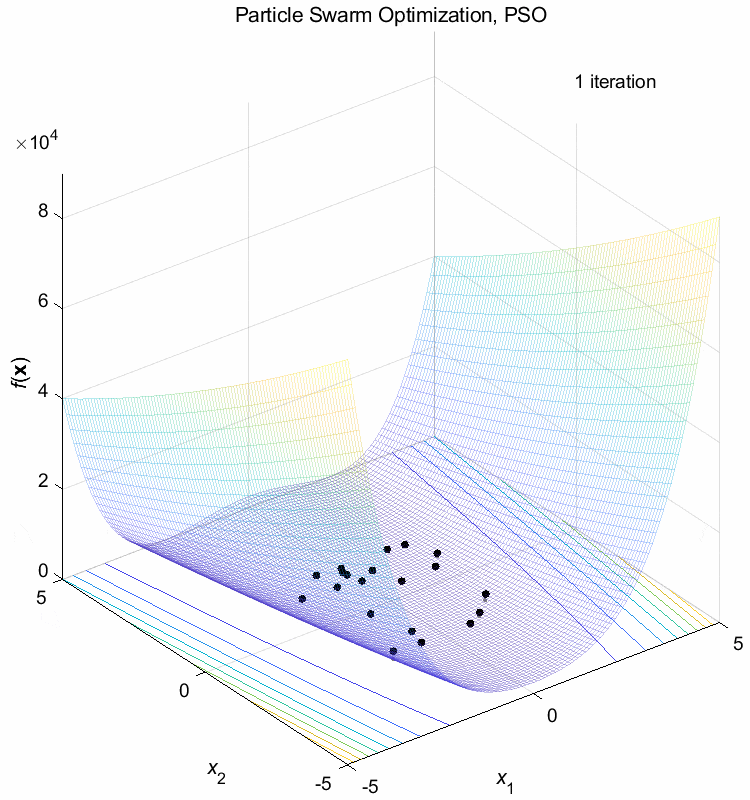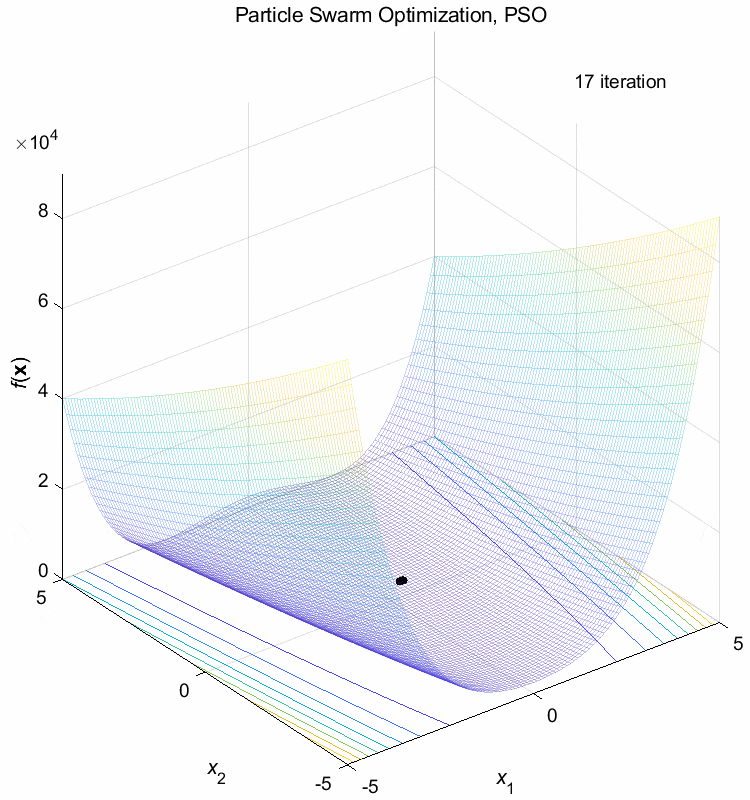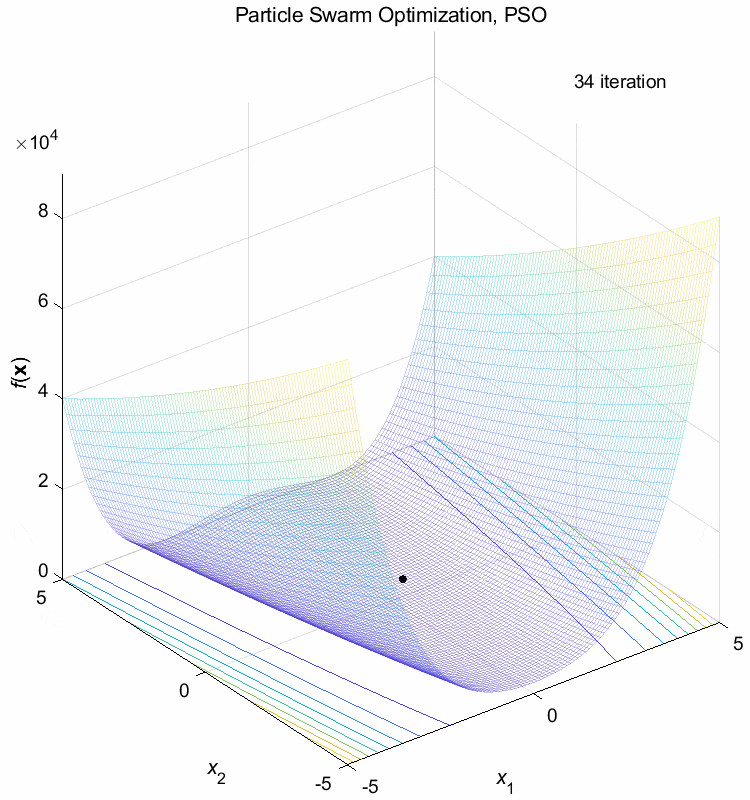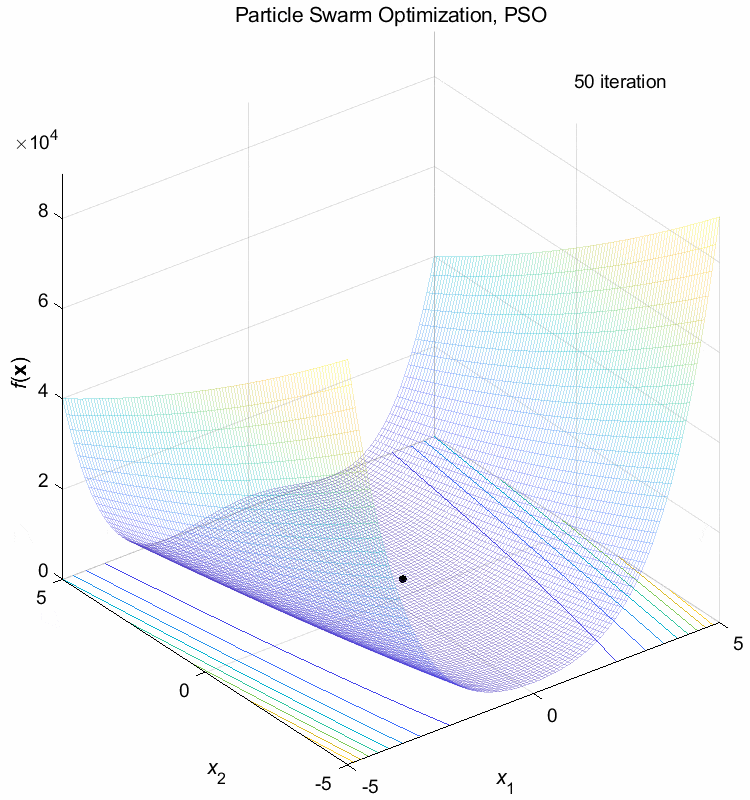
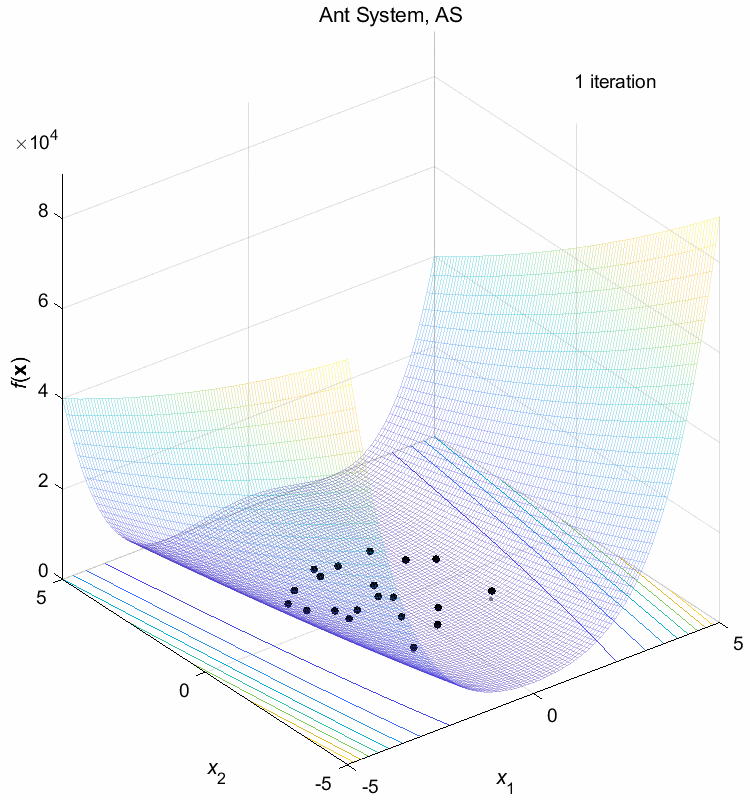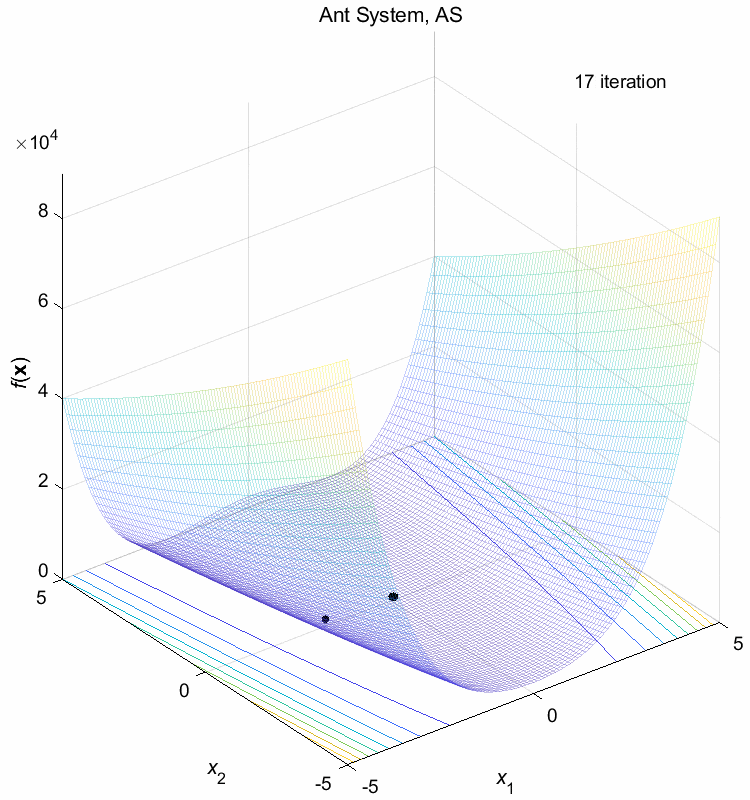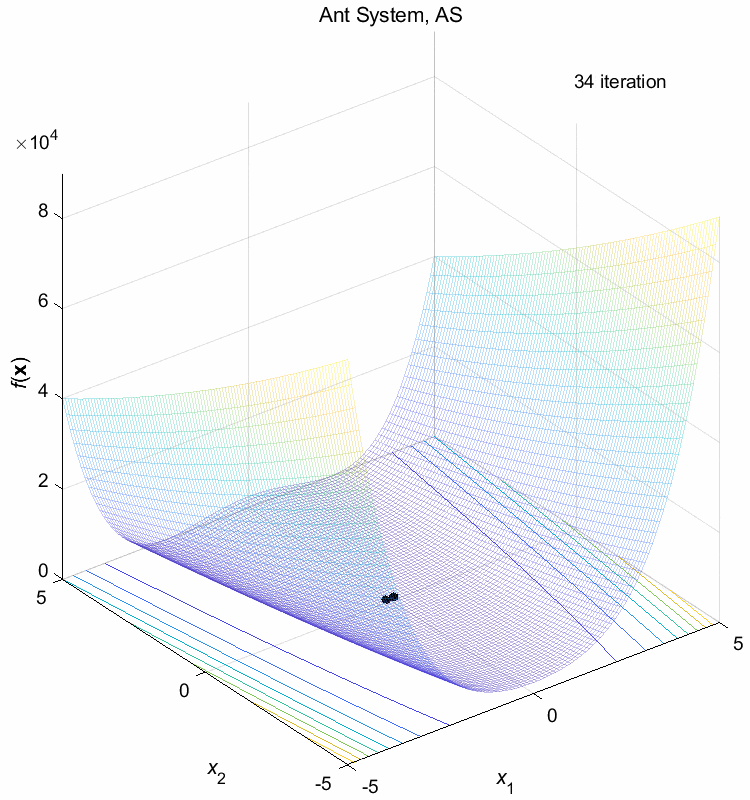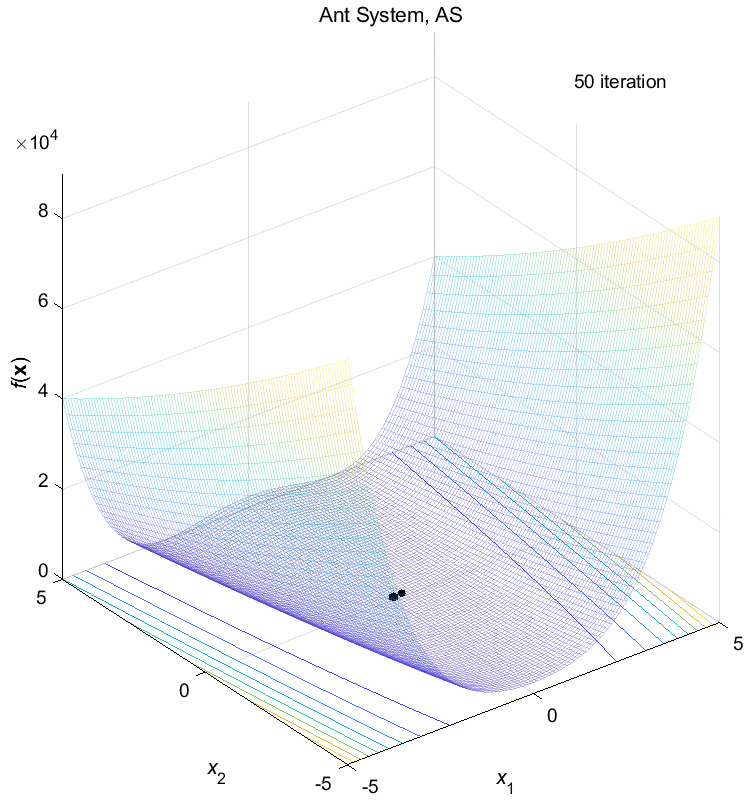
Rosenbrock function:
\(\text{Minimize } f(\boldsymbol{x}) = \sum_{i=1}^{n-1} (100(x_{i+1}-x_i^2)^2+(1-x_i)^2)\)
\(-5 \leq x_i \leq 5\) \(f(\boldsymbol{x}^*) = f(1,1,\dots,1)=0\)
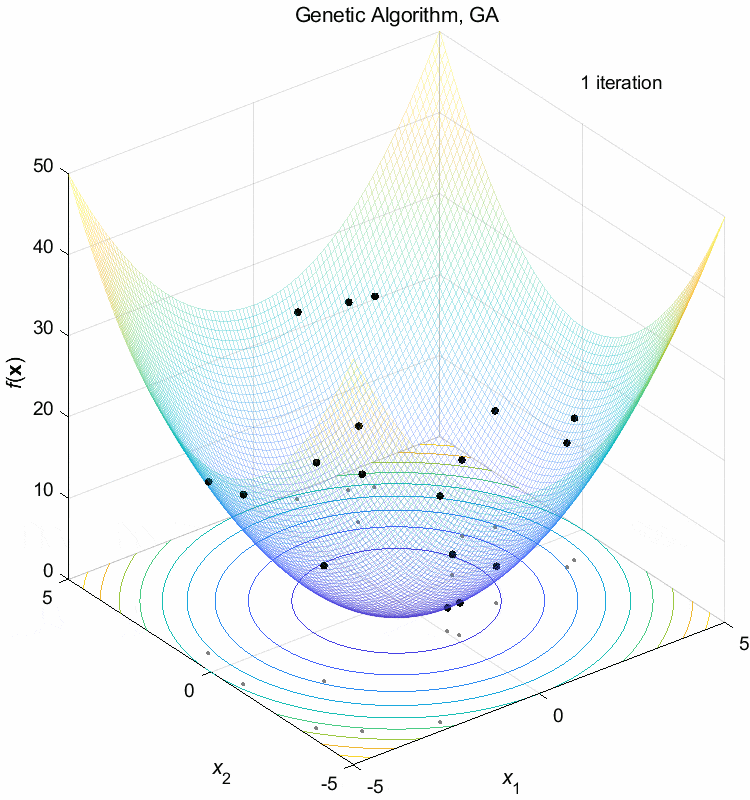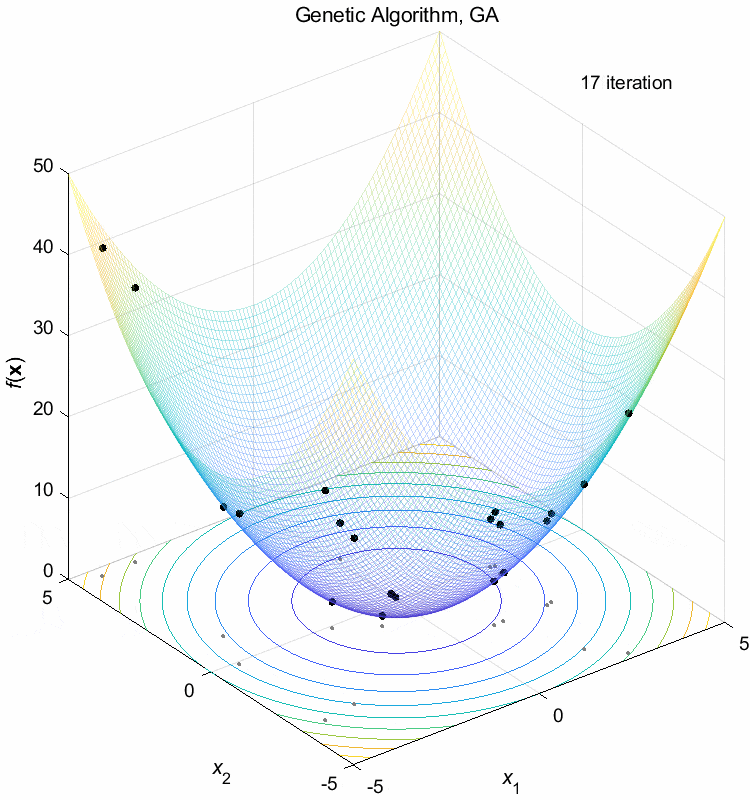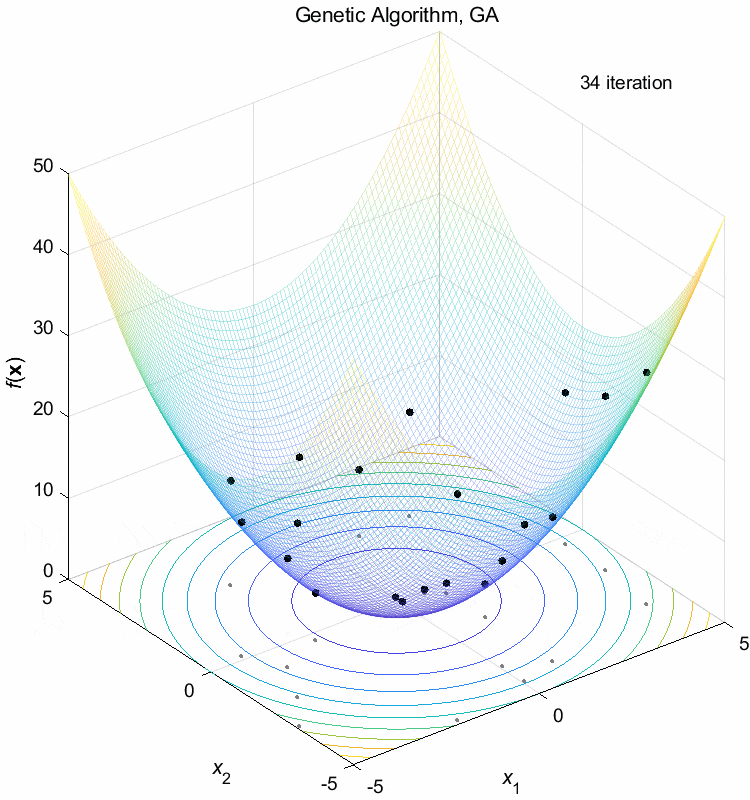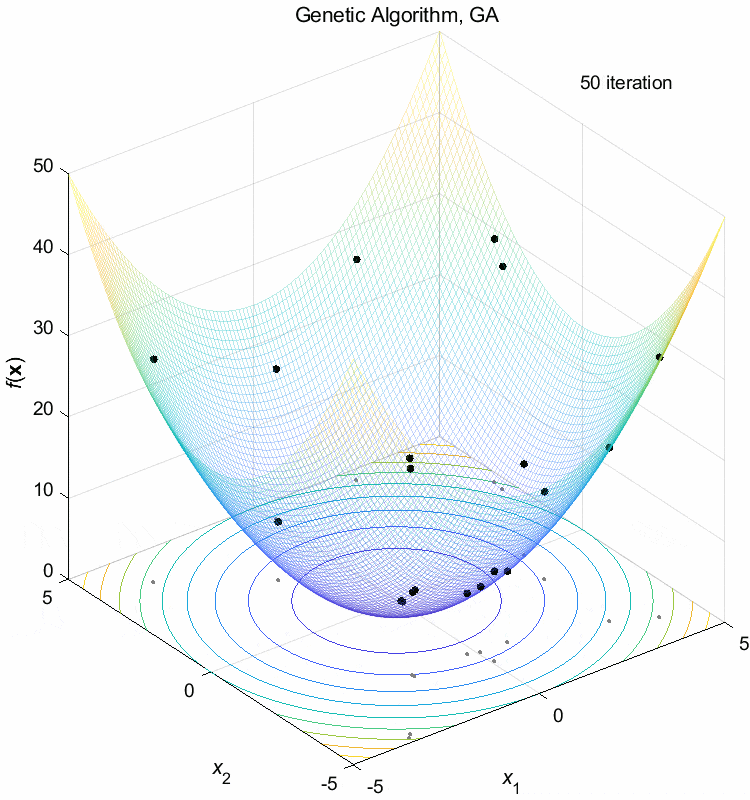
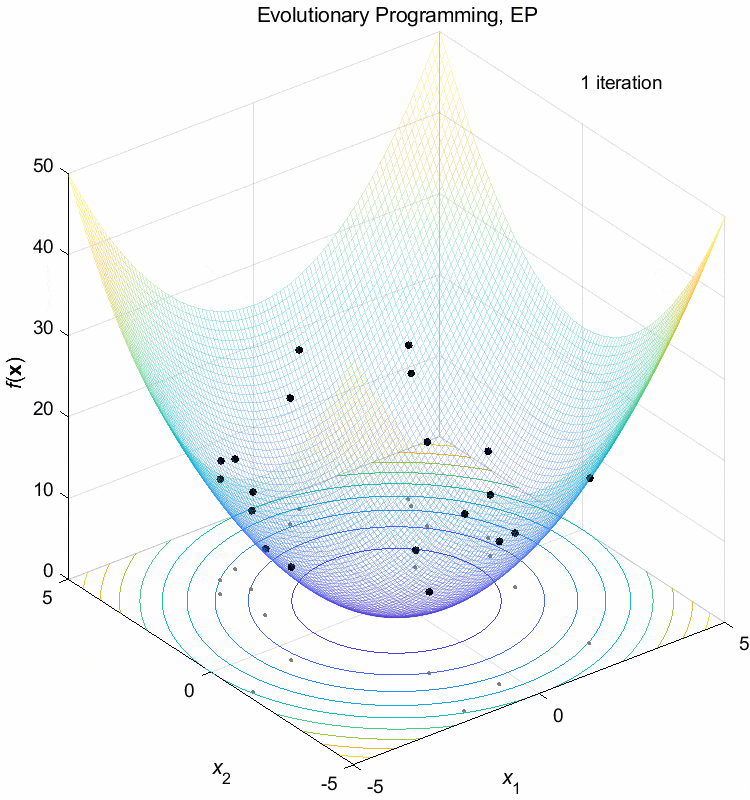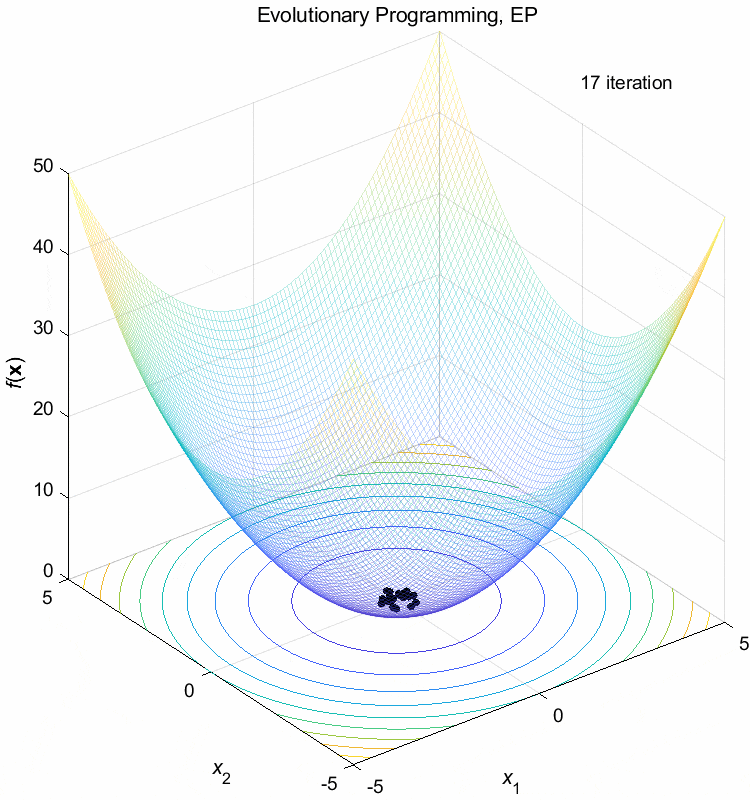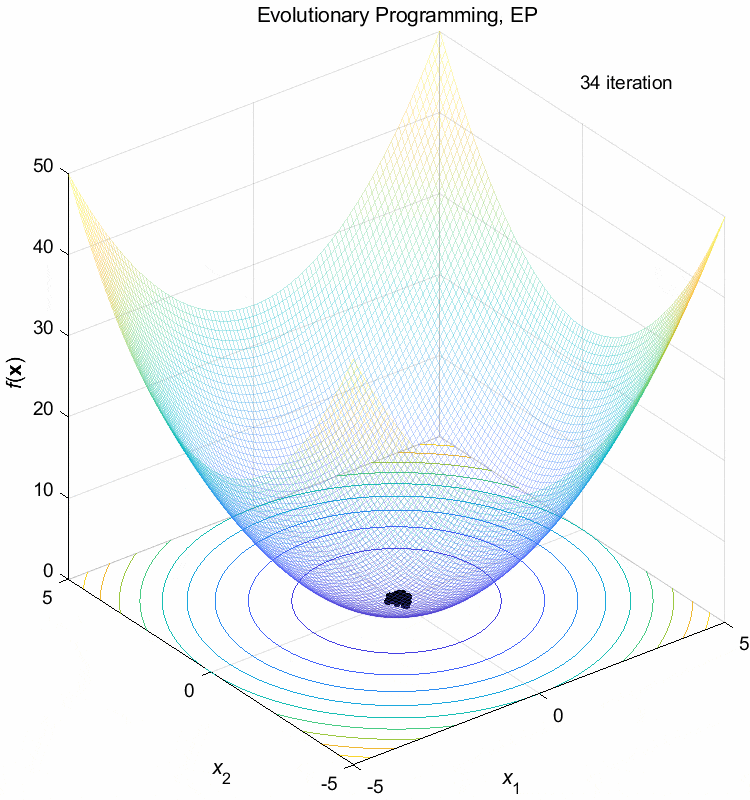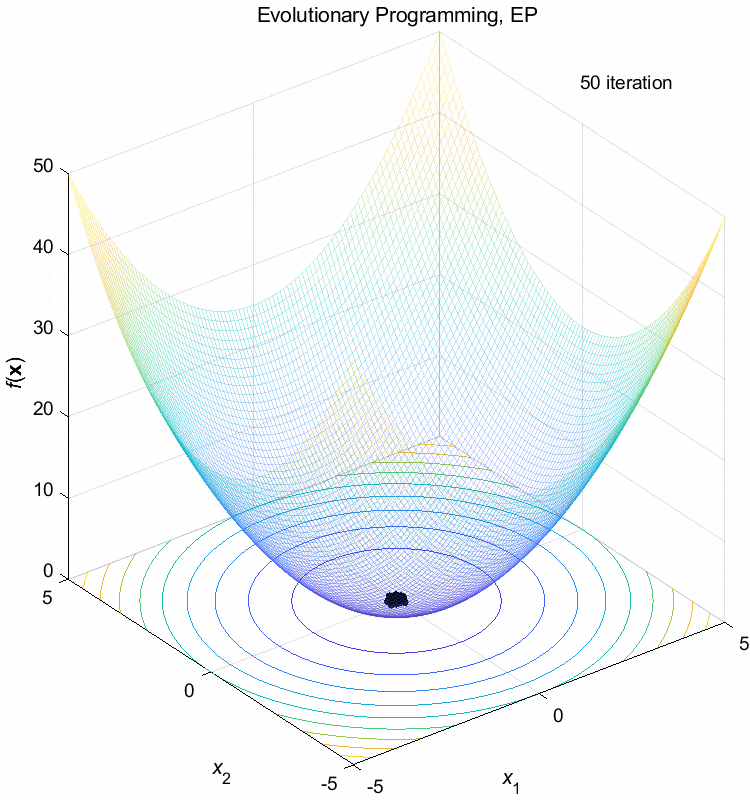
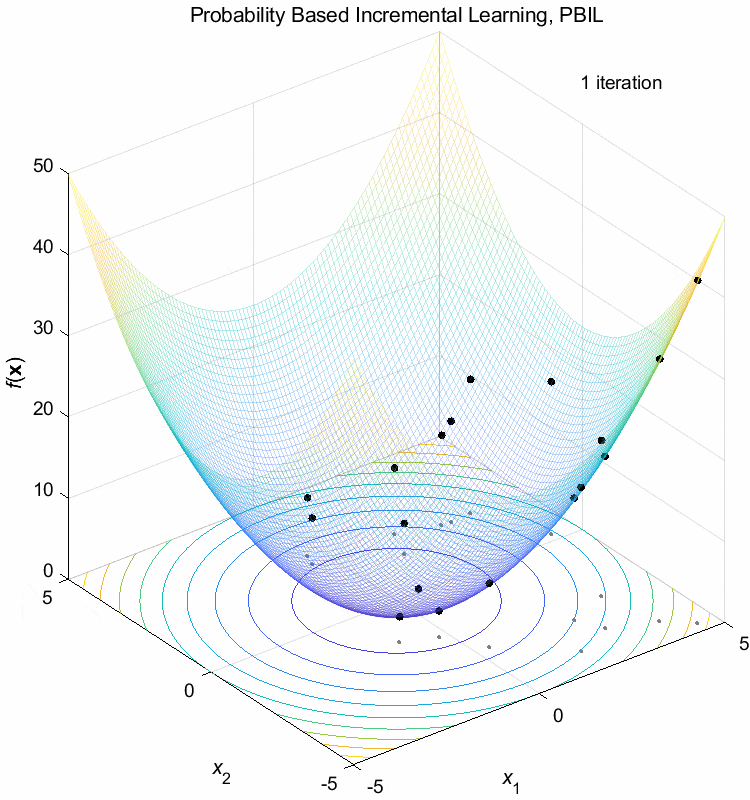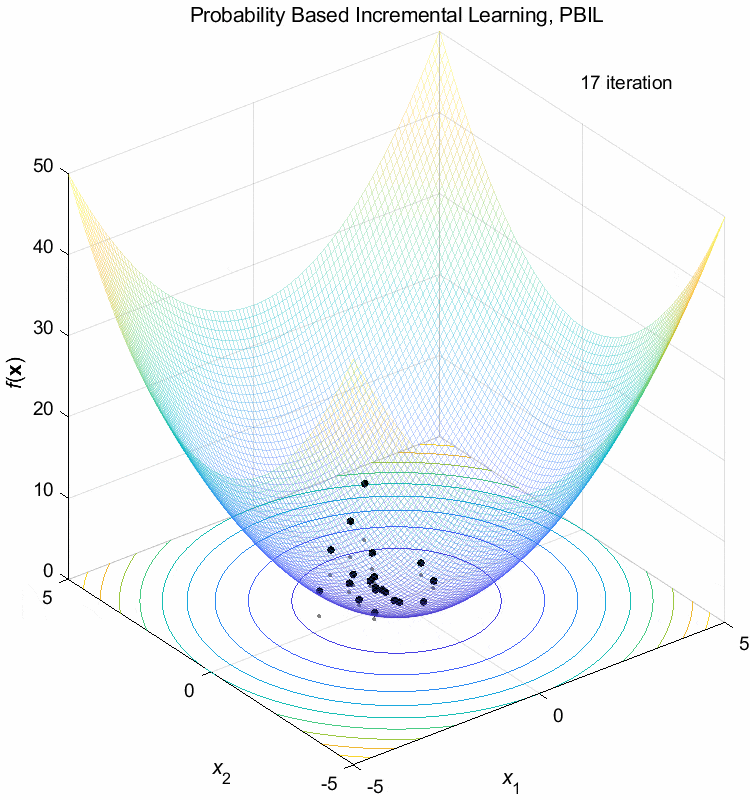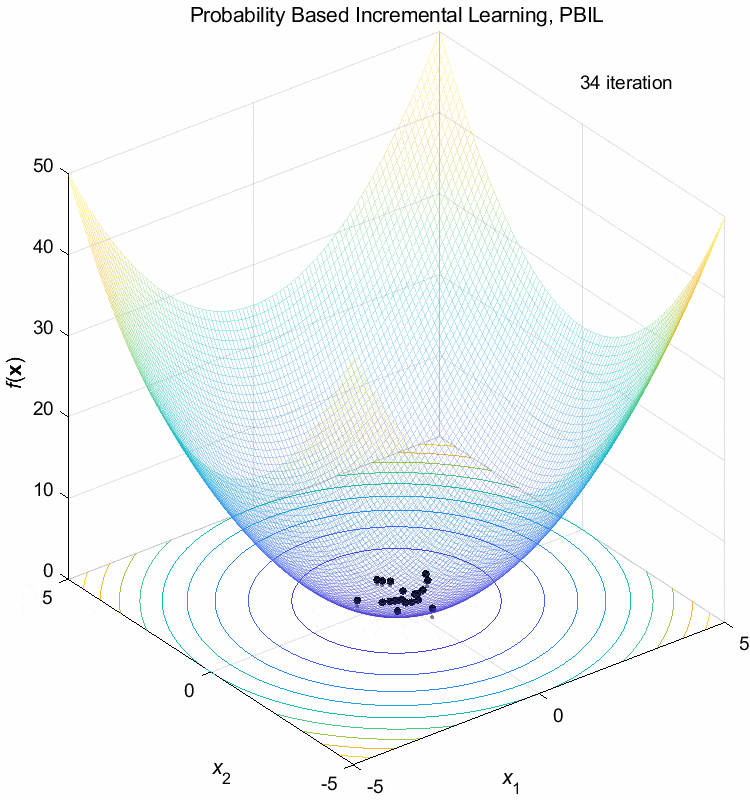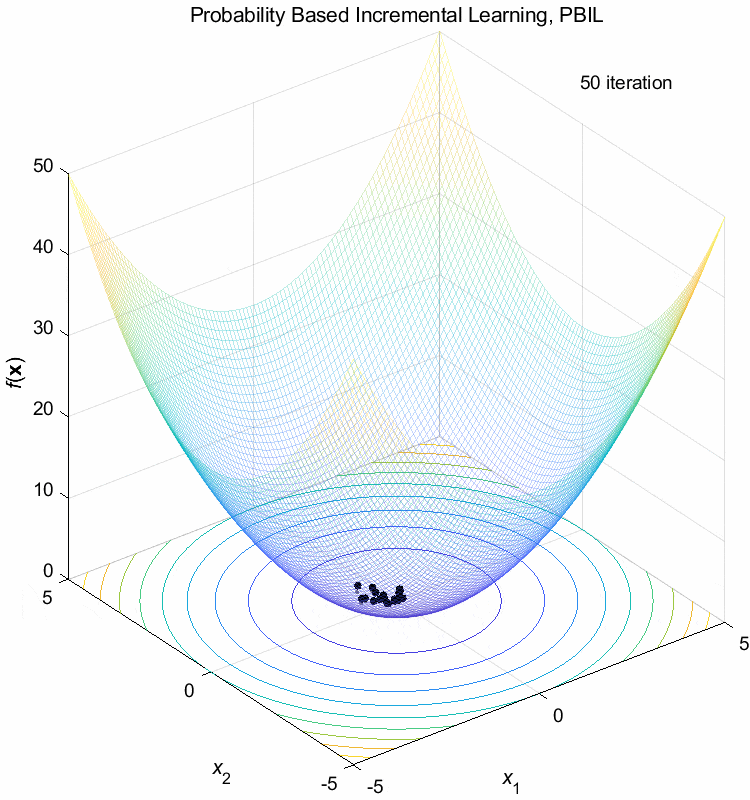
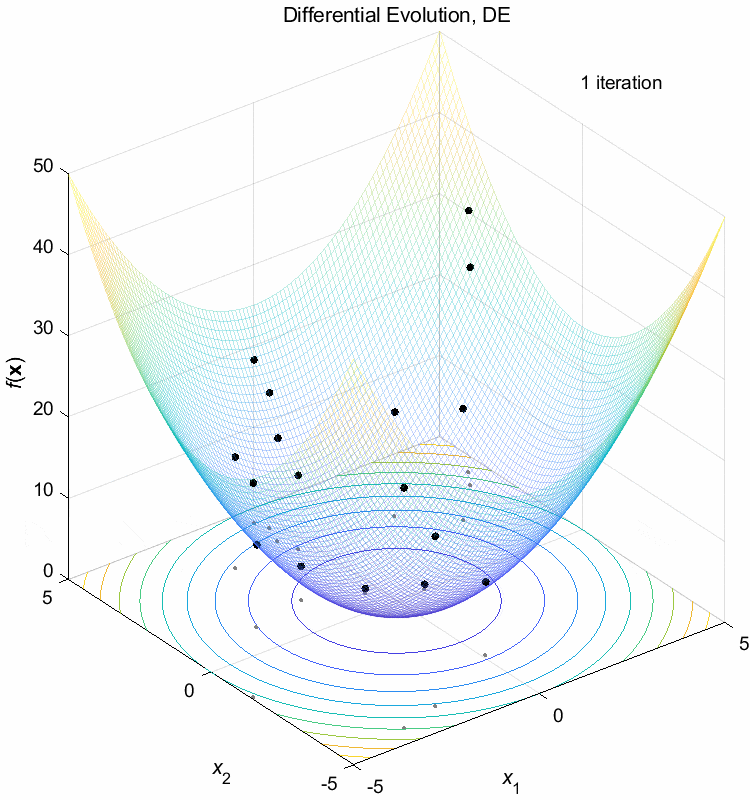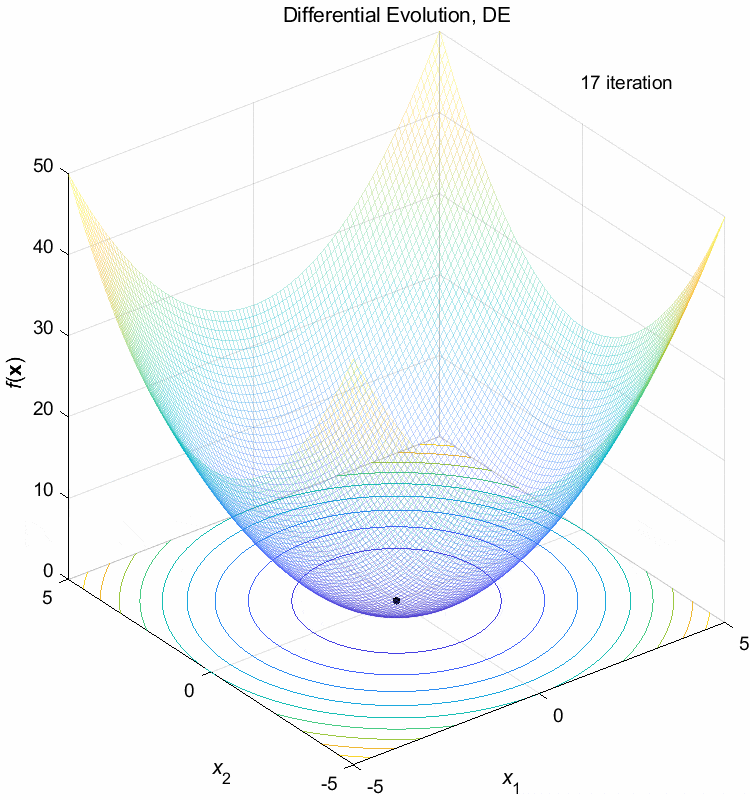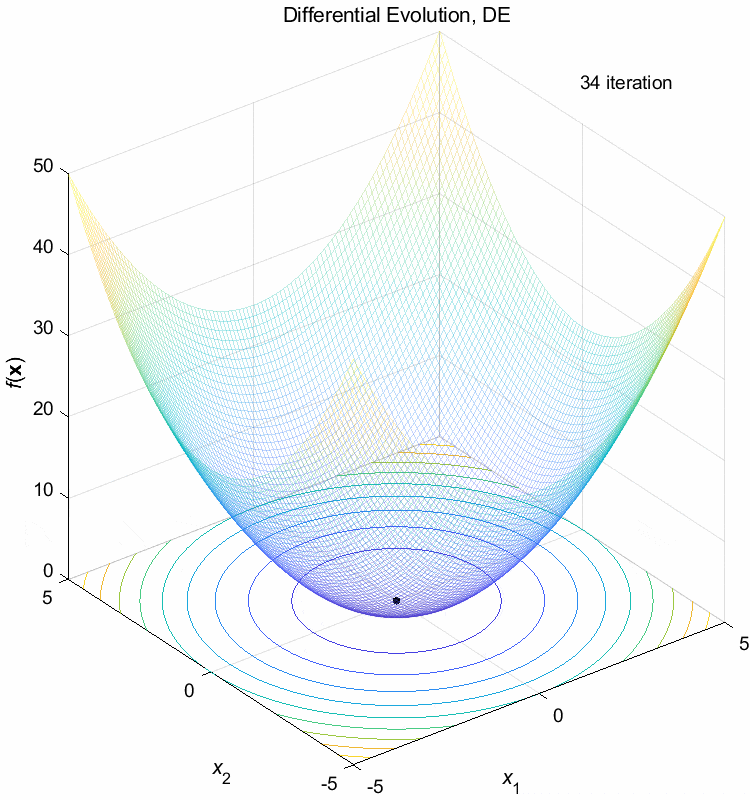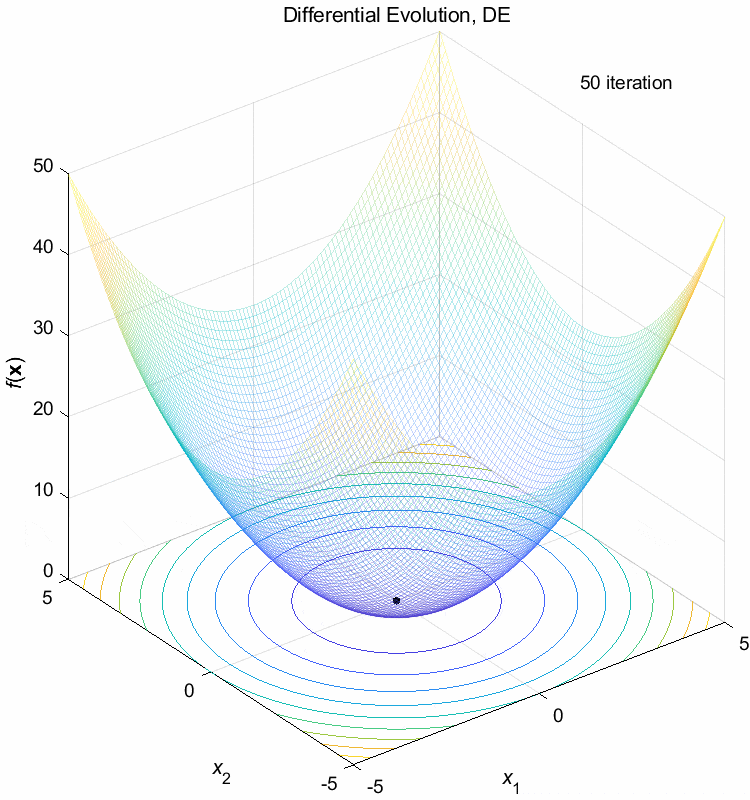
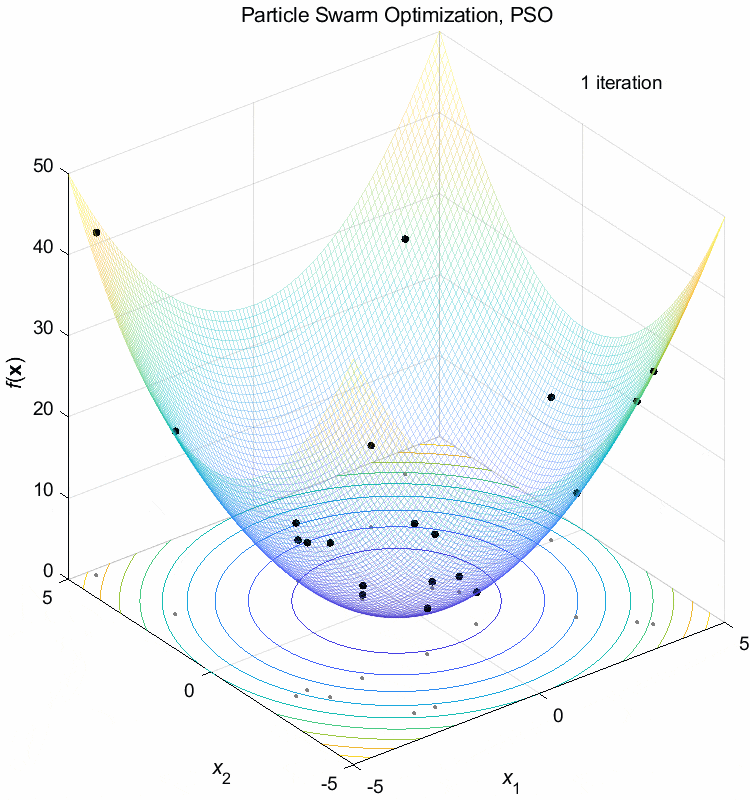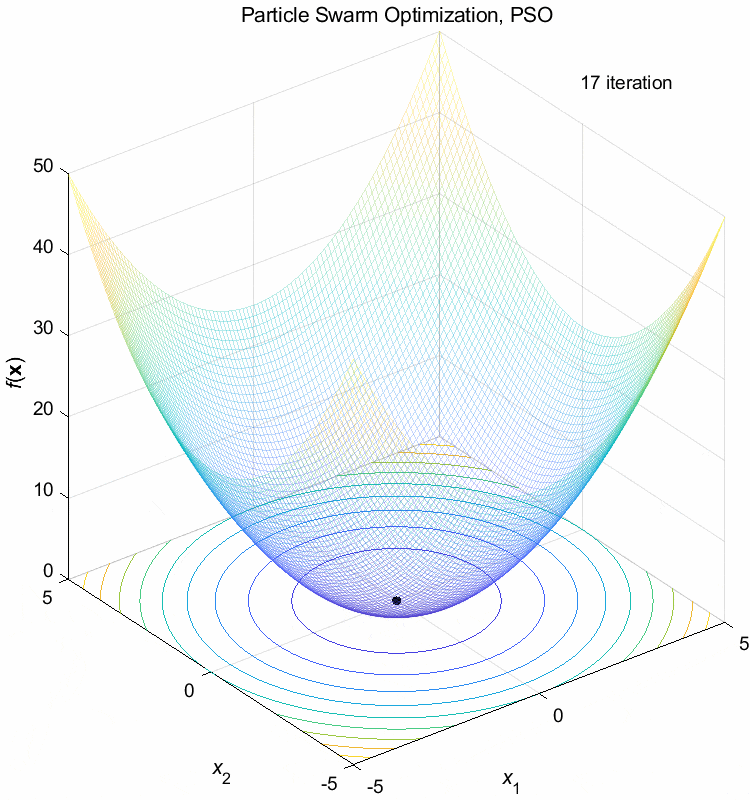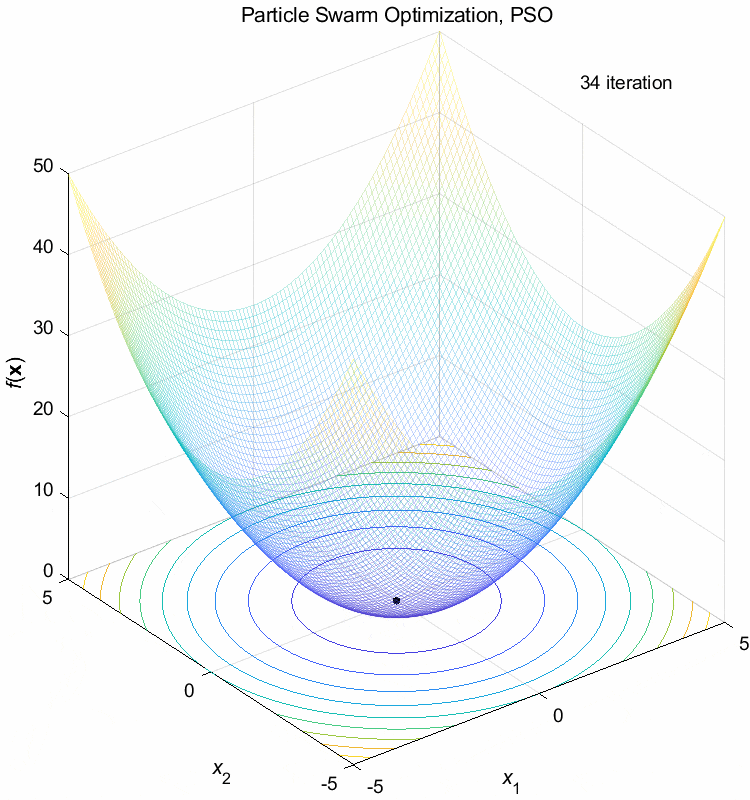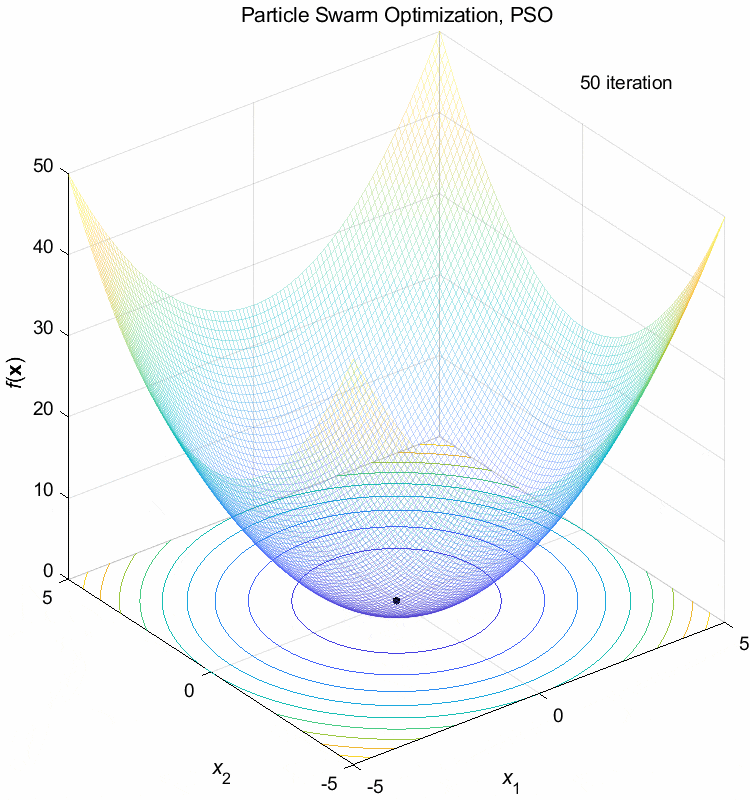
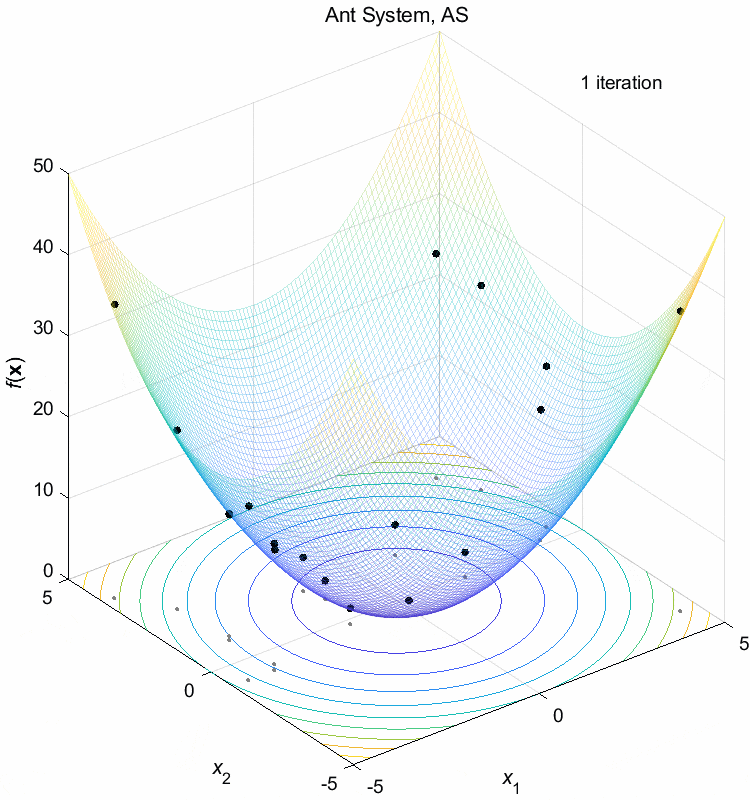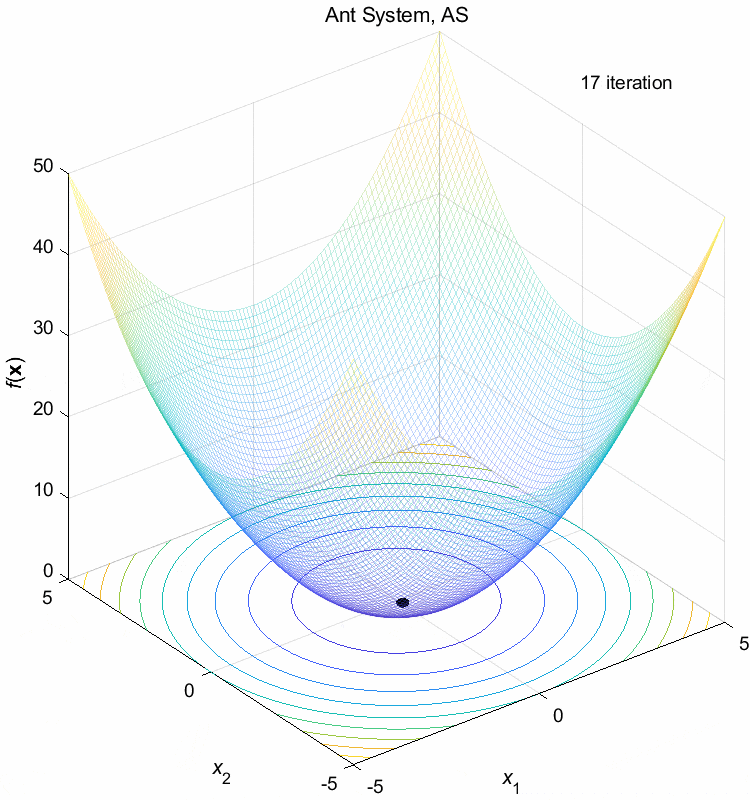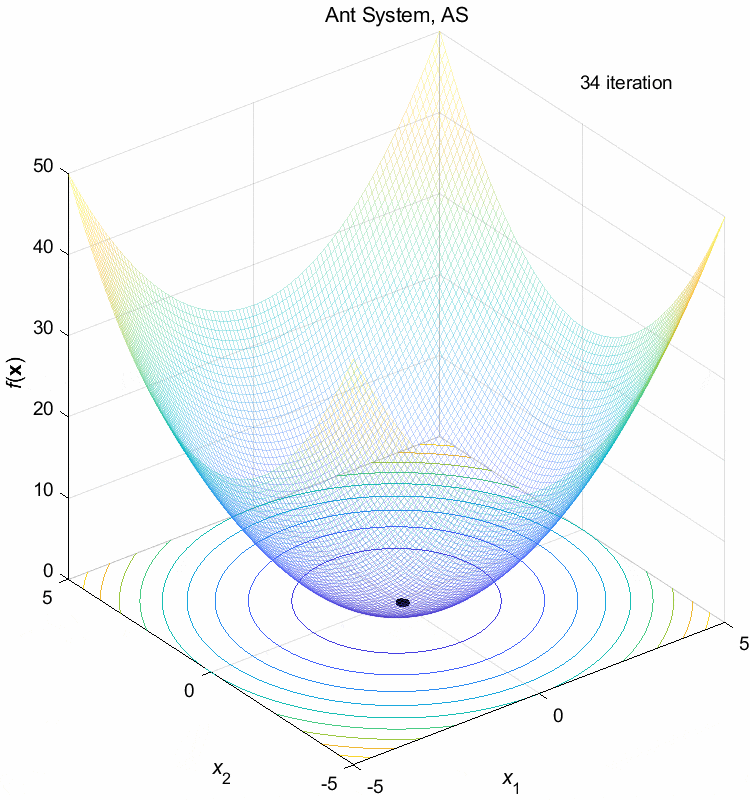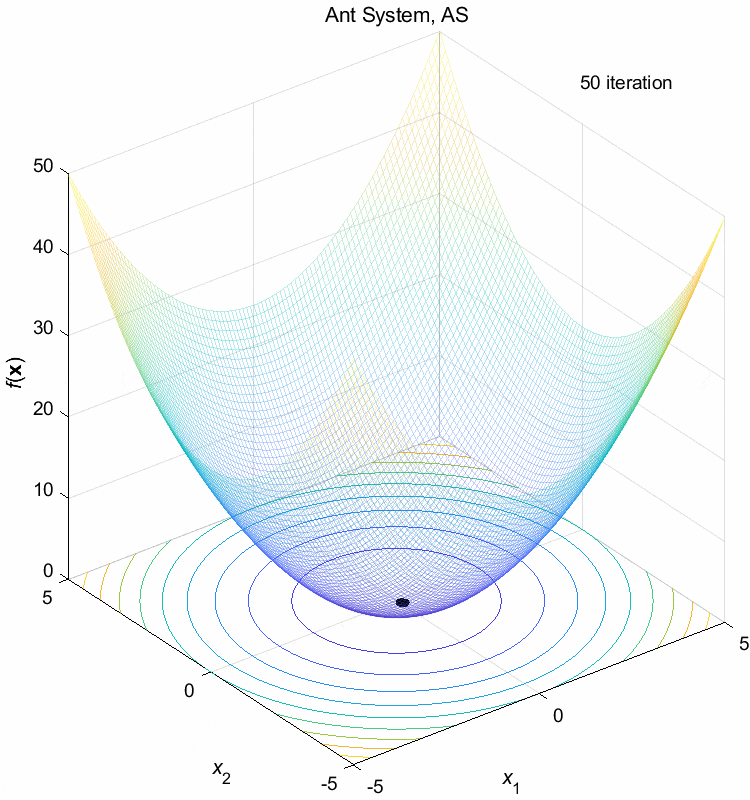
Sphere function:
\(\text{Minimize } f(\boldsymbol{x}) = \sum_{i=1}^n x_i^2\)
\(-5 \leq x_i \leq 5\) \(f(\boldsymbol{x}^*) = f(0,0,\dots,0)=0\)
Javascript Animations
Weight Vector Generation Method
You can change the weight vector size in the animation
- Simplex-lattice design
- Incremental lattice design
- Riesz 𝑠-energy
- Hammersley method
Weight Vector Change Methods
You can change the weight vector distribution in the animation
- Change method 1
- Change method 2
- Change method 3
- Change method 4
- Normalized change method 1 (This distribution does not change)
- Normalized change method 2
- Normalized change method 3
- Normalized change method 4